广东省深圳市南山区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 对称美在生活中处处可见，下列是历届冬奥会的会徽，其中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在平行四边形ABCD中，CE⊥AB，E为垂足，如果∠D＝64°，则∠BCE等于（）

A、26° B、30° C、36° D、64°

查看试题解析
3. 如图，∠ABD=∠CBD，AB=CB，据此可以证明 $△$ BAD≌ $△$ BCD，依据是（）

A、AAS B、ASA C、SAS D、HL

查看试题解析
4. 下列从左边到右边的变形中，是因式分解的是（）

A、 $(x + 3) (x - 3) = x^{2} - 9$ B、 $a^{2} - a - 6 = a (a - 1) - 6$ C、 $y^{2} - 1 = (y + 1) (y - 1)$ D、 $3 x + 1 = x (3 + \frac{1}{x})$

查看试题解析
5. 若不等式 $(m + 2) x > m + 2$ 的解集是 $x < 1$ ，则m的取值范围是（）.

A、 $m > 0$ B、 $m < 0$ C、 $m > - 2$ D、 $m < - 2$

查看试题解析
6. 如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AB＝16，将△ABC沿CB方向向右平移得到△DEF，若四边形ABED的面积为24，则平移距离是（）

A、2 B、3 C、4 D、6

查看试题解析
7. 下列式子中正确的是（）

A、 $\frac{a^{2}}{a b} = \frac{a}{b}$ B、 $\frac{a}{b} = \frac{a + 1}{b + 1}$ C、 $\frac{a}{b} = \frac{a - 1}{b - 1}$ D、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$

查看试题解析
8. 如图，直线 $y = k x + b (k \neq 0)$ 经过点 $(- 1 ， 3)$ ，则不等式 $k x + b \geq 3$ 的解集为（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x \geq 3$ D、 $x \geq - 1$

查看试题解析
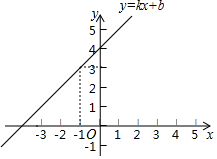9. 如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．
步骤1∶以C为圆心，CA为半径画弧①；

步骤2∶以B为圆心，BA为半径画弧②，交弧①于点D；

步骤3∶连接AD，交BC延长线于点H．

下列叙述正确的是（）

A、BH垂直平分线段AD B、AC平分∠BAD C、S_△ABC=BC⋅AH D、AB=AD

查看试题解析
10. 如图，四边形ABCD中．AC⊥BC， $A D$ // $B C$ ， BD为∠ABC的平分线，BC＝6，AC＝8．E、F分别是BD、AC的中点，则EF的长为（）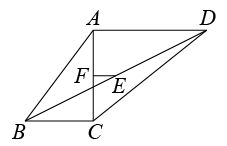

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 当x时，分式 $\frac{1}{x - 5}$ 有意义.

查看试题解析
12. 因式分解： $x^{2} - 6 x + 9$ =.

查看试题解析
13. 如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，若BC＝8，DE＝3，则BD的长为．

查看试题解析
14. 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠1＋∠2＋∠3＋∠4＝290°，则∠D＝．

查看试题解析
15. 对于任意两个非零实数a、b，定义新运算“*”如下： $a * b = \frac{1}{b} - \frac{1}{a}$ ，例如： $3 * 4 = \frac{1}{4} - \frac{1}{3} = - \frac{1}{12}$ ．若x*y＝2，则 $\frac{2022 x y}{x - y}$ 的值为．

查看试题解析

三、解答题

16.

(1)、解不等式： $3 x - 2 \geq x + 1$

(2)、解不等式组： ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析

17. 计算

\frac{x^{2}}{x + 1} - x + 1

时，小明、小亮两位同学的解法如下：

小明： $\frac{x^{2}}{x + 1} - x + 1$

$= \frac{x^{2}}{x + 1} - \frac{x + 1}{1}$ ①

$= \frac{x^{2}}{x + 1} - \frac{{(x + 1)}^{2}}{x + 1}$ ②

小亮： $\frac{x^{2}}{x + 1} - x + 1$

$= \frac{x^{2}}{x + 1} - \frac{x}{1} + \frac{1}{1}$ ③

$= \frac{x^{2}}{x + 1} - \frac{x (x + 1)}{x + 1} + \frac{x + 1}{x + 1}$ ④

(1)、判断：小明、小亮两位同学的解题过程有无错误？若无误，请直接跳到下一问；若有误，则找出最先出错的式子：（填序号）．

(2)、请任选一种自己喜欢的解法，完成解答．

查看试题解析

18. 如图，在12×12正方形网格中建立直角坐标系，每个小正方形的边长为1个单位长度，△ABC的三个顶点的坐标依次为：A（0，2），B（－3，5），C（－2，2）．

(1)、将△ABC以点A为旋转中心旋转180°，得到 $△ A B_{1} C_{1}$ ，点B、C的对应点分别为点 $B_{1}$ 、 $C_{1}$ ，请在网格图中画出 $△ A B_{1} C_{1}$ ．

(2)、将△ABC平移至 $△ A_{2} B_{2} C_{2}$ ，其中点A、B、C的对应点分别为点 $A_{2}$ 、 $B_{2}$ 、 $C_{2}$ ，且点 $C_{2}$ 的坐标为（－2，－4），请在图中画出平移后的 $△ A_{2} B_{2} C_{2}$ ．

(3)、在第（1）、（2）小题基础上，若将 $△ A B_{1} C_{1}$ 绕某一点旋转可得到 $△ A_{2} B_{2} C_{2}$ ，则旋转中心的坐标为．（直接写出答案）

查看试题解析
19. 如图，在四边形ABCD中，AB＝CD，∠ABC的平分线交AD于点E，与CD的延长线交于点F，BC＝FC．

(1)、求证：四边形ABCD是平行四边形；

(2)、若AB＝5，BC＝8，CE⊥AD，求平行四边形ABCD面积．

查看试题解析
20. 我们学习了一元一次不等式（组）的解法，请阅读学习一元二次不等式的解题思想方法，并以此解决后面的问题．
课题学习：如何解一元二次不等式？
例题：解一元二次不等式 $x^{2} - 4 > 0$ ．
解：将 $x^{2} - 4$ 分解因式
$x^{2} - 4 = (x + 2) (x - 2)$
∵ $x^{2} - 4 > 0$
∴ $(x + 2) (x - 2) > 0$
根据有理数的乘法法则：“两数相乘，同号得正”，
则有：（1） ${\begin{array}{l} x + 2 > 0 \\ x - 2 > 0 \end{array}$ 或（2） ${\begin{array}{l} x + 2 < 0 \\ x - 2 < 0 \end{array}$
解不等式组（1）得： $x > 2$
解不等式组（2）得： $x < - 2$
∴ $(x + 2) (x - 2) > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ．
即：一元二次不等式 $x^{2} - 4 > 0$ 的解集为 $x > 2$ 或 $x < - 2$ ．
课题总结：解一元二次不等式的过程，体现了数学的化归思想及分类讨论思想．
问题解决：

(1)、解一元二次不等式 $x^{2} - 3 x > 0$

(2)、类比一元二次不等式的解题思想方法，直接写出分式不等式 $\frac{2 x + 1}{x - 5} < 0$ 的解集为：．

查看试题解析
21. 南山荔枝，中国国家地理标志产品，品种多样，其中糯米糍是最受大家喜爱的品种．某水果店上午购进了一批总价为4800元的糯米糍，很快销售一空．下午，水果店老板又补购了2000元的糯米糍，单价每斤比上午便宜了4元，并且下午的补货量恰好是上午的一半．

(1)、糯米糍上午的进价是多少元/斤？

(2)、上午和下午按相同的价格出售，若售完总利润率不低于20%，则销售单价至少为多少元/斤？

查看试题解析
22. 如图1，△ABC是边长为4cm的等边三角形，边AB在射线OM上，且OA＝6cm，点D从点O出发，沿射线OM方向以1cm/s的速度运动，当D不与点A重合时，将线段CD绕点C逆时针方向旋转60°得到CE，连接DE、BE，设点D运动了ts．

(1)、点D的运动过程中，线段AD与BE的数量关系是，请以图1情形为例（当点D在线段OA上时，点D与点A不重合），说明理由．

(2)、当6<t<10时，如图2，△BDE周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由．

(3)、当点D在射线OM上运动时，是否存在以D、B、E为顶点的三角形是直角三角形？若存在，直接写出此时t的值．

查看试题解析