广东省深圳市龙华区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 则下列结论正确的是( )A、a-3>b-3 B、 C、 D、3. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、4. 如图,是边长为2的等边三角形,将沿直线平移至的位置,连接 , 则的长是( )
2. 若 , 则下列结论正确的是( )A、a-3>b-3 B、 C、 D、3. 下列各式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、4. 如图,是边长为2的等边三角形,将沿直线平移至的位置,连接 , 则的长是( ) A、 B、2 C、 D、35. 若分式中a,b都扩大到原来的2倍,则分式的值( )A、保持不变 B、缩小到原来的倍 C、扩大到原来的2倍 D、无法确定6. 不等式的解集在数轴上表示正确的是( )A、
A、 B、2 C、 D、35. 若分式中a,b都扩大到原来的2倍,则分式的值( )A、保持不变 B、缩小到原来的倍 C、扩大到原来的2倍 D、无法确定6. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,在中,边的垂直平分线交于E,交于点D,若 , , 则的周长为( )
7. 如图,在中,边的垂直平分线交于E,交于点D,若 , , 则的周长为( ) A、8 B、9 C、7 D、108. 下列命题是真命题的是( )A、六边形的内角和与外角和都是 B、等腰三角形的高、中线、角平分线互相重合 C、一组对边平行且另一组对边相等的四边形是平行四边形 D、斜边和一条直角边分别相等的两个直角三角形全等9. 为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15500元,已知每个足球60元,每个篮球90元,学校最多可以购买的篮球个数是( )A、115 B、116 C、117 D、11810. 如图,在中, , 将绕顶点A逆时针旋转至 , 此时点D在上,连接 , 线段分别交于点H、K,则下列四个结论中:①;②是等边三角形;③;④当时,;正确的是( )
A、8 B、9 C、7 D、108. 下列命题是真命题的是( )A、六边形的内角和与外角和都是 B、等腰三角形的高、中线、角平分线互相重合 C、一组对边平行且另一组对边相等的四边形是平行四边形 D、斜边和一条直角边分别相等的两个直角三角形全等9. 为进一步落实“德、智、体、美、劳”五育并举工作,某中学以体育为突破口,准备从体育用品商场一次性购买若干个足球和篮球,用于学校球类比赛活动.根据学校实际情况,需一次性购买足球和篮球共200个,但要求足球和篮球的总费用不超过15500元,已知每个足球60元,每个篮球90元,学校最多可以购买的篮球个数是( )A、115 B、116 C、117 D、11810. 如图,在中, , 将绕顶点A逆时针旋转至 , 此时点D在上,连接 , 线段分别交于点H、K,则下列四个结论中:①;②是等边三角形;③;④当时,;正确的是( ) A、①②④ B、①③④ C、②③④ D、①②③
A、①②④ B、①③④ C、②③④ D、①②③二、填空题
-
11. 分解因式: =12. 要使分式有意义,x的取值应满足的条件是 .13. 我们定义一种新运算: , 如 , 则关于a的不等式的最大整数解为 .14. 用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,称为平面图形的镶嵌.某工人师傅把四块完全相同的平面图形按如图所示的方式进行镶嵌,经测量, , , B、D两点之间的距离为 , 则图中阴影部分的面积为 .
 15. 如图,在中, , , AD平分 , 过点B作于点E,F是边上一动点,连接 , 当时,的长是 .
15. 如图,在中, , , AD平分 , 过点B作于点E,F是边上一动点,连接 , 当时,的长是 .
三、解答题
-
16.(1)、解不等式组:(2)、解方程: .17. 先化简、再求值: , 其中 .18. 在长度均为1的正方形网格中建立如图所示的平面直角坐标系,已知点A、B、C的坐标分别为 .
 (1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .19. 如图,在平行四边形中,点H是边上一点,连接 .
(1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .19. 如图,在平行四边形中,点H是边上一点,连接 . (1)、尺规作图:请作出的角平分线,分别交于点G、E,交的延长线于点F.(不写作法,保留作图痕迹)(2)、若点G恰好是线段的中点,求证: .20. 某鲜花店销售A种鲜花每束的单价比B种多6元,张阿姨发现:用720元购得的A种鲜花与用600元购得的B种鲜花的束数一样多.母亲节前夕,该鲜花店推出优惠活动方案:购买A种鲜花,前10束(含10束)按原价销售,购买超过10束,每多买一束,送一束;购买B种鲜花,每束都按原价的七五折销售.(1)、求该鲜花店A、B两种鲜花的单价各是多少元?(2)、某公司准备购进m束(m为大于10的偶数)同种鲜花,请问该如何购买更合算?请通过计算说明.21. 【问题背景】
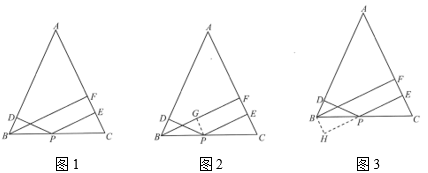
(1)、尺规作图:请作出的角平分线,分别交于点G、E,交的延长线于点F.(不写作法,保留作图痕迹)(2)、若点G恰好是线段的中点,求证: .20. 某鲜花店销售A种鲜花每束的单价比B种多6元,张阿姨发现:用720元购得的A种鲜花与用600元购得的B种鲜花的束数一样多.母亲节前夕,该鲜花店推出优惠活动方案:购买A种鲜花,前10束(含10束)按原价销售,购买超过10束,每多买一束,送一束;购买B种鲜花,每束都按原价的七五折销售.(1)、求该鲜花店A、B两种鲜花的单价各是多少元?(2)、某公司准备购进m束(m为大于10的偶数)同种鲜花,请问该如何购买更合算?请通过计算说明.21. 【问题背景】某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交的延长线于点H;
 (1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】
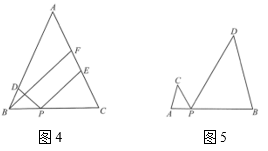
(1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】如图4,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
(3)、 【拓展应用】如图5,在与中, , , 点A、B、P在同一条直线上,若 , , 则 .
22. 如图1,在四边形中, , ; (1)、求证:四边形为平行四边形;(2)、如图2所示,将四边形沿着折叠,使得点D落在边上,连接 , 当时,则;(3)、在(2)的条件下,以点A为原点,边所在的直线为x轴建立平面直角坐标系,将沿射线方向平移得到 , 如图3所示,若点B的坐标为 , 点D的坐标为 , 则在这个平移过程中,点、B、是否可以构成等腰三角形?若可以,请直接写出点的坐标,若不可以,请说明理由.
(1)、求证:四边形为平行四边形;(2)、如图2所示,将四边形沿着折叠,使得点D落在边上,连接 , 当时,则;(3)、在(2)的条件下,以点A为原点,边所在的直线为x轴建立平面直角坐标系,将沿射线方向平移得到 , 如图3所示,若点B的坐标为 , 点D的坐标为 , 则在这个平移过程中,点、B、是否可以构成等腰三角形?若可以,请直接写出点的坐标,若不可以,请说明理由.