广东省深圳市光明区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 古希腊哲学家毕达哥拉斯曾说:“美的线型和其他一切美的形体,都必须有对称形式.”下面以数学家名字命名的图形中,是中心对称图形的是( )A、谢尔宾斯基三角形
 B、科克曲线
B、科克曲线 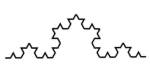 C、赵爽弦图
C、赵爽弦图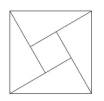 D、毕达哥拉斯树
D、毕达哥拉斯树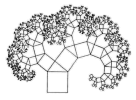 2. 分式有意义的条件是( )A、 B、 C、 D、x为任意实数3. 五边形的内角和是( )A、180° B、360° C、540° D、720°4. 多项式中各项的公因式是( )A、ab B、4ab C、 D、5. 不等式的解集在数轴上表示正确的是( )A、
2. 分式有意义的条件是( )A、 B、 C、 D、x为任意实数3. 五边形的内角和是( )A、180° B、360° C、540° D、720°4. 多项式中各项的公因式是( )A、ab B、4ab C、 D、5. 不等式的解集在数轴上表示正确的是( )A、 B、
B、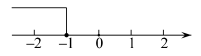 C、
C、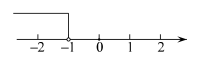 D、
D、 6. 下列由左边到右边的变形是因式分解的是( )A、 B、 C、 D、7. 下列说法正确的是( )A、四边形的外角和是360° B、如果 , 那么 C、点关于原点对称的点的坐标是 D、一组对边相等,另一组对边平行的四边形是平行四边形8. 直线与在同一平面直角坐标系中的图像如图所示,则关于x的不等式的解集为( )
6. 下列由左边到右边的变形是因式分解的是( )A、 B、 C、 D、7. 下列说法正确的是( )A、四边形的外角和是360° B、如果 , 那么 C、点关于原点对称的点的坐标是 D、一组对边相等,另一组对边平行的四边形是平行四边形8. 直线与在同一平面直角坐标系中的图像如图所示,则关于x的不等式的解集为( ) A、 B、 C、 D、9. 如图,点P在∠AOB的平分线上, PC⊥OA于点C, ∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( )
A、 B、 C、 D、9. 如图,点P在∠AOB的平分线上, PC⊥OA于点C, ∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( ) A、3 B、2 C、1 D、10. 如图,AC是▱ABCD的对角线,将▱ABCD折叠,使得点A与点C重合,再将其打开展平,得折痕EF,EF与AC交于点O,G为CF的中点,连接OG、CE.则下列结论:①;②;③;④ . 其中正确的有( )
A、3 B、2 C、1 D、10. 如图,AC是▱ABCD的对角线,将▱ABCD折叠,使得点A与点C重合,再将其打开展平,得折痕EF,EF与AC交于点O,G为CF的中点,连接OG、CE.则下列结论:①;②;③;④ . 其中正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 因式分解: ;12. 分式方程的增根为 .13. 如果将点A(-3,-1)向右平移2个单位长度,再向下平移3个单位得到点B,那么点B的坐标是 .14. 如图,在△ABC中, , , 边BC的垂直平分线DE分别交AB、BC于点E、D,则△ACE的周长为 .
 15. 如图,在▱ABCD中, , , M为AB的中点, , 点E是线段CM上一个动点,以CD为对角线作▱CEDF,则EF的最小值是 .
15. 如图,在▱ABCD中, , , M为AB的中点, , 点E是线段CM上一个动点,以CD为对角线作▱CEDF,则EF的最小值是 .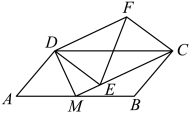
三、解答题
-
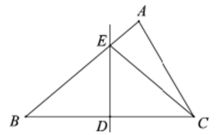
16. 解不等式组 .17. 解分式方程 .18. 先化简,再求值: ,其中 .19. 如图,D是△ABC的边BC的中点, , , 垂足分别是E、F,且 .
 (1)、求证:△ABC是等腰三角形;(2)、若 , , 求△ABC的面积.20. 北京冬奥会吉祥物冰墩墩和雪容融受到大家的喜爱.某冬奥商品授权经销店欲购进这两种纪念品,已知每件冰墩墩的进价比雪容融的进价贵10元,用450元购进冰墩墩的数量与用360元购进雪容融的数量相同.(1)、求冰墩墩和雪容融每件的进价分别为多少元?(2)、若该商店冰墩墩纪念品每件售价65元,雪容融纪念品每件售价50元,这两种纪念品共购进200件,全部售出后总获利不低于2400元,求雪容融纪念品最多购进多少件?21. 如图1,直线与x轴、y轴分别交于点C和点B,已知点 .
(1)、求证:△ABC是等腰三角形;(2)、若 , , 求△ABC的面积.20. 北京冬奥会吉祥物冰墩墩和雪容融受到大家的喜爱.某冬奥商品授权经销店欲购进这两种纪念品,已知每件冰墩墩的进价比雪容融的进价贵10元,用450元购进冰墩墩的数量与用360元购进雪容融的数量相同.(1)、求冰墩墩和雪容融每件的进价分别为多少元?(2)、若该商店冰墩墩纪念品每件售价65元,雪容融纪念品每件售价50元,这两种纪念品共购进200件,全部售出后总获利不低于2400元,求雪容融纪念品最多购进多少件?21. 如图1,直线与x轴、y轴分别交于点C和点B,已知点 .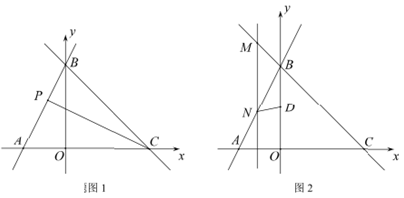 (1)、求直线AB的解析式;(2)、P为线段AB上一个动点,若 , 求此时点P的坐标;(3)、点D是BO的中点,M为直线BC上的一个动点,过M为作轴交直线AB于点N,若以B、D、M、N为顶点的四边形是平行四边形,求出所有符合条件的M点的坐标.22. △ABC和△DEC是等腰直角三角形, , , .
(1)、求直线AB的解析式;(2)、P为线段AB上一个动点,若 , 求此时点P的坐标;(3)、点D是BO的中点,M为直线BC上的一个动点,过M为作轴交直线AB于点N,若以B、D、M、N为顶点的四边形是平行四边形,求出所有符合条件的M点的坐标.22. △ABC和△DEC是等腰直角三角形, , , .
 (1)、【观察猜想】当△ABC和△DEC按如图1所示的位置摆放,连接BD、AE,延长BD交AE于点F,猜想线段BD和AE有怎样的数量关系和位置关系.(2)、【探究证明】如图2,将△DCE绕着点C顺时针旋转一定角度 , 线段BD和线段AE的数量关系和位置关系是否仍然成立?如果成立,请证明:如果不成立,请说明理由.(3)、【拓展应用】如图3,在△ACD中, , , , 将AC绕着点C逆时针旋转90°至BC,连接BD,求BD的长.
(1)、【观察猜想】当△ABC和△DEC按如图1所示的位置摆放,连接BD、AE,延长BD交AE于点F,猜想线段BD和AE有怎样的数量关系和位置关系.(2)、【探究证明】如图2,将△DCE绕着点C顺时针旋转一定角度 , 线段BD和线段AE的数量关系和位置关系是否仍然成立?如果成立,请证明:如果不成立,请说明理由.(3)、【拓展应用】如图3,在△ACD中, , , , 将AC绕着点C逆时针旋转90°至BC,连接BD,求BD的长.