广东省揭阳市普宁市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 将图中可爱的“小鸭子”图片按逆时针方向旋转90°后得到的图片是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,数轴上所表示关于x的不等式组的解集是( )
2. 如图,数轴上所表示关于x的不等式组的解集是( ) A、 B、 C、 D、3. 如图,在四边形ABCD中,对角线AC,BD交于点O,ADBC,添加如下一个条件,使四边形ABCD为平行四边形(不添加任何辅助线),其中错误的是( ).
A、 B、 C、 D、3. 如图,在四边形ABCD中,对角线AC,BD交于点O,ADBC,添加如下一个条件,使四边形ABCD为平行四边形(不添加任何辅助线),其中错误的是( ). A、AD=BC B、AB=CD C、AO=CO D、ABCD4. 一个多边形的每一个外角都等于 ,则这个多边形的边数 等于( )A、8 B、10 C、12 D、145. 要把分式方程化为整式方程,方程两边要同时乘以( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、(x+y)(x﹣y)=x2﹣y2 B、x2﹣y2=(x+y)(x﹣y) C、(x+y) 2=x2+y2 D、x2+y2=(x+y)27. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )
A、AD=BC B、AB=CD C、AO=CO D、ABCD4. 一个多边形的每一个外角都等于 ,则这个多边形的边数 等于( )A、8 B、10 C、12 D、145. 要把分式方程化为整式方程,方程两边要同时乘以( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、(x+y)(x﹣y)=x2﹣y2 B、x2﹣y2=(x+y)(x﹣y) C、(x+y) 2=x2+y2 D、x2+y2=(x+y)27. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )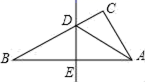 A、10cm B、12cm C、15cm D、17cm8. 一次函数 的图象如图所示,则不等式 的解集是( )
A、10cm B、12cm C、15cm D、17cm8. 一次函数 的图象如图所示,则不等式 的解集是( ) A、 B、 C、 D、9. 下列命题的逆命题是假命题是( )A、两直线平行,同旁内角互补 B、平行四边形的对边平行且相等 C、如果 , 那么或 D、如果两个角是对顶角,那么它们相等10. 如图,已知平行四边形ABCD中,3AB=2BC,点O是∠BAD和∠CBA的角平分线的交点,过点O作EF AB,分别交AD、BC于E、F两点,连接OD、OC.则下列结论:①AO⊥BO;②点O是EF的中点;③DE=2AE;④S△OCD=4S△OAE , 其中正确的有( )
A、 B、 C、 D、9. 下列命题的逆命题是假命题是( )A、两直线平行,同旁内角互补 B、平行四边形的对边平行且相等 C、如果 , 那么或 D、如果两个角是对顶角,那么它们相等10. 如图,已知平行四边形ABCD中,3AB=2BC,点O是∠BAD和∠CBA的角平分线的交点,过点O作EF AB,分别交AD、BC于E、F两点,连接OD、OC.则下列结论:①AO⊥BO;②点O是EF的中点;③DE=2AE;④S△OCD=4S△OAE , 其中正确的有( )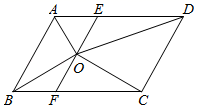 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式: .12.
如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
 13. 若 , 则的值是 .14. 分式方程的解是 .15. 如图,在▱ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
13. 若 , 则的值是 .14. 分式方程的解是 .15. 如图,在▱ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .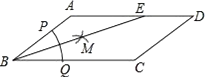 16. 如图,在 中, ,过点B作 ,交 于点D , 若 ,则 的长度为 .
16. 如图,在 中, ,过点B作 ,交 于点D , 若 ,则 的长度为 . 17. 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),点B在第一象限角平分线上,且BA⊥x轴,现将点A、B绕点O同时逆时针匀速旋转,当点A绕点O旋转90°到达y轴上的点C时,点B刚好绕点O旋转了45°到达y轴上的点D'处.则当点A旋转一周回到(2,0)时,点B所在的位置坐标为 .
17. 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),点B在第一象限角平分线上,且BA⊥x轴,现将点A、B绕点O同时逆时针匀速旋转,当点A绕点O旋转90°到达y轴上的点C时,点B刚好绕点O旋转了45°到达y轴上的点D'处.则当点A旋转一周回到(2,0)时,点B所在的位置坐标为 .
三、解答题
-
18. 先化简,再求值 ,其中 .19. 解不等式组 , 并在数轴上表示出不等式组的解集.20. 如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O,
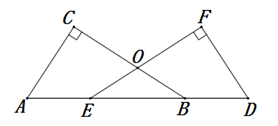 (1)、求证:Rt△ABC≌Rt△DEF;(2)、若∠A=51°,求∠BOF的度数.21. 如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)、求证:Rt△ABC≌Rt△DEF;(2)、若∠A=51°,求∠BOF的度数.21. 如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.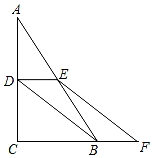 (1)、求证:四边形DEFB是平行四边形;(2)、若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.22. 某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、现在商城准备一次性购进这两种家电共100台,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,一共有多少种合理的购买方案?23. 阅读与思考:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如:四项的多项式一般按照“两两”分组或“三一”分组,进行分组分解.
(1)、求证:四边形DEFB是平行四边形;(2)、若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.22. 某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、现在商城准备一次性购进这两种家电共100台,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,一共有多少种合理的购买方案?23. 阅读与思考:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如:四项的多项式一般按照“两两”分组或“三一”分组,进行分组分解.例1:“两两分组”:
解:原式
例2:“三一分组”:
解:原式
归纳总结:用分组分解法分解因式要先恰当分组,然后用提公因式法或运用公式法继续分解.请同学们在阅读材料的启发下,解答下列问题:
(1)、分解因式:①;
②;
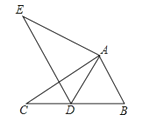
(2)、已知的三边a,b,c满足 , 试判断的形状.24. 已知M是等边的边BC上的点.
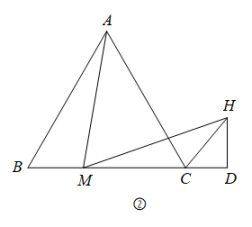 (1)、如图①,过点M作 , 交AB于点N,求证:;(2)、如图②,连接AM,过点M作 , MH与的邻补角的平分线交于点H,过点H作 , 交BC延长线于点D.求证:;(3)、在(2)的条件下,猜想CB,CM,CD之间的数量关系,并证明.25. 如图,在 ABCD中,AE⊥BC于点E,BE=3,AB=5,连接AC,点F以每秒1个单位长度的速度由点A向点C匀速运动,到达C点即停止运动,G,H分别是AF,EF的中点,连接GH.设点F运动的时间为t.
(1)、如图①,过点M作 , 交AB于点N,求证:;(2)、如图②,连接AM,过点M作 , MH与的邻补角的平分线交于点H,过点H作 , 交BC延长线于点D.求证:;(3)、在(2)的条件下,猜想CB,CM,CD之间的数量关系,并证明.25. 如图,在 ABCD中,AE⊥BC于点E,BE=3,AB=5,连接AC,点F以每秒1个单位长度的速度由点A向点C匀速运动,到达C点即停止运动,G,H分别是AF,EF的中点,连接GH.设点F运动的时间为t. (1)、判断GH与AE的位置关系和数量关系,并求出GH的长;(2)、若CE=AB.
(1)、判断GH与AE的位置关系和数量关系,并求出GH的长;(2)、若CE=AB.①求点F由点A向点C匀速运动的过程中,线段GH所扫过区域的面积;
②若△FGH是等腰三角形,求t的值.