广东省惠州市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 若式子 $\frac{x}{\sqrt{3 x - 4}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq \frac{4}{3}$ B、 $x > \frac{4}{3}$ C、 $x ≥ \frac{3}{4}$ D、 $x > \frac{3}{4}$

查看试题解析
2. 下列各曲线中不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
3. 在今年新型冠状病毒肺炎疫情防疫工作中，庆阳某中学为了了解八（1）班学生某天的体温情况，班长把所有同学当天上报的体温（单位：℃）绘制成了如下统计表：
体温（℃）
35.8
36.1
36.2
36.3
36.4
36.5
36.6
36.8
人数（人）
3
4
8
8
10
8
2
2
这组体温数据的众数是（）

A、36.4℃ B、36.2℃ C、36.3℃ D、36.5℃

查看试题解析
4. 下列计算结果正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ D、 $\frac{\sqrt{2}}{\sqrt{5}} = 5 \sqrt{10}$

查看试题解析
5. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了几步路，却踩伤了花草，他们少走的路长为（）

A、 $2 m$ B、 $3 m$ C、 $3.5 m$ D、 $4 m$

查看试题解析
6. 下列条件中，使 $△ A B C$ 不是直角三角形的是（）

A、 $a = 5 ， b = 12 ， c = 13$ B、 $a ： b ： c = 1 ： \sqrt{3} ： 2$ C、 $a^{2} + b^{2} = c^{2}$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
7. 如图，在▱ABCD中，AB $⊥$ AC，若AB=4，AC=6，则BD的长是（）

A、11 B、10 C、9 D、8

查看试题解析
8. 在函数 $y = k x + b$ （其中k、b为常数，且 $k < 0$ ）的图象上有 $A (1 ， y_{1}) ， B (- 2 ， y_{2})$ 两个点，则下列各式中正确的是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} \leq y_{2}$ C、 $y_{1} > y_{2}$ D、 $y_{1} \geq y_{2}$

查看试题解析
9. 如图，正方形 $A B C D$ 的边长为3， $△ A B E$ 是等边三角形，点E在正方形 $A B C D$ 内，在对角线 $A C$ 上有一点P，使 $P D + P E$ 的和最小，则这个最小值为（）

A、 $\sqrt{6}$ B、 $2 \sqrt{3}$ C、3 D、2

查看试题解析
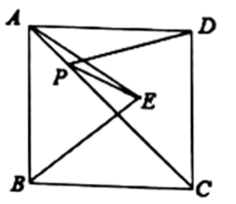10. 如图，正方形 $A B C D$ 的边长为4，P为正方形边上一动点，运动路线是 $A \to D \to C \to B \to A$ ，设点P经过的路程为x，以点A、P、D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $\sqrt{20 a}$ 为正整数，则满足条件的a的最小正整数值为

查看试题解析
12. 已知样本数据为6，7，9，8，10，则这5个数的方差是．

查看试题解析
13. 菱形的两条对角线长分别是6和8，则此菱形的面积是．

查看试题解析
14. 点 $P (a ， b)$ 在函数 $y = 3 x - 1$ 的图象上，则代数式 $6 a - 2 b + 2022$ 的值等于．

查看试题解析
15. 如图， $R t △ A B C ， ∠ C = 90 ° ， A C = 8 c m ， B C = 6 c m ， C D$ 是 $A B$ 边上的高，则 $C D =$ $c m$ ．

查看试题解析
16. 直线l₁：y=k₁x+b与直线l2：y=k₂x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k₂x > k₁x+b的解集为

查看试题解析
17. 如图，正方形 $A B C D$ 中，点E是 $A B$ 上一点，点F在 $B C$ 的延长线上，且 $A E = C F$ ，连接 $D E ， D F ， E F ， B D$ ，其中 $E F$ 交 $C D$ 于点G，下列结论：① $∠ D E F = 45 °$ ；② $△ B C D ≌ △ E D F$ ；③若 $A B = 3 ， A E = \frac{1}{3} A B$ ，则 $S_{△ D E F} = 5$ ；④若E为 $A B$ 的中点，则 $\frac{E F}{B D} = \frac{\sqrt{10}}{2}$ ．其中正确的结论是（填写所有正确结论的序号）

查看试题解析

三、解答题

18. 计算： $(\sqrt{54} + \sqrt{24}) \div \sqrt{12} - \sqrt{\frac{1}{8}} \times (2 \sqrt{2})^{2}$ ．

查看试题解析
19. 如图，已知 $▱$ ABCD中，E、F分别是AD、BC边上的点，DE＝BF，求证：AF $/ /$ CE.

查看试题解析
20. 如图， $R t △ A B C ， ∠ C = 90 ° ， A C = 8 ， B C = 4$ ．

(1)、尺规作图：作 $A B$ 的垂直平分线交 $A C$ 于点D，交 $A B$ 于点E（不写作法，保留作图痕迹）；

(2)、在（1）的基础上，连接 $B D$ ，求 $B D$ 的长．

查看试题解析
21. 已知：四边形 $A B C D$ 中， $A C ⊥ B C ， A B = 8 ， B C = 4 ， C D = 6 ， D A = 2 \sqrt{3}$ ．

(1)、求 $A C$ 的长；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
22. 甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如图所示的尚不完整的统计图表（其中图①中“10分”所在扇形圆心角为 $90 °$ ）．
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8

(1)、在图①中，求“7分”所在扇形的圆心角度数：并将②的统计图补充完整；

(2)、经计算，乙校的平均分是8.3分，中位数是8分，请求出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好；

(3)、如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？

查看试题解析
23. 我国正在迈入“5G时代”，而我们的华为在5G核心专利上排世界第一，引来美国对华为的打压，国家从上而下都在支持华为，某手机店准备进一批华为手机，经调查，用80000元采购A型华为手机的台数和用60000元采购B型华为手机的台数一样，一台A型华为手机的进价比一台B型华为手机的进价多800元．

(1)、求一台A，B型华为手机的进价分别为多少元？

(2)、若手机店购进A，B型华为手机共60台进行销售，其中A型华为手机的台数不大于B型华为手机的台数，且不小于20台，已知A型华为手机的售价为4200元/台，B型华为手机的售价为2800元/台，且全部售出，手机店怎样安排进货，才能在销售这批华为手机时获最大利润，求出最大利润．

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = \frac{1}{2} x + 3$ 分别与x轴、y轴交于点B、C，且与直线 $y = - \frac{1}{2} x$ 交于A．

(1)、分别求出A、B、C的坐标；

(2)、若D是线段 $O A$ 上的点，且 $△ C O D$ 的面积为3，求直线 $C D$ 的函数解析式；

(3)、在（2）的条件下，设P是射线 $C D$ 上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析
25. 如图1，在同一平面内，把一个含 $45 °$ 角的直角三角板 $E C F$ 和一个正方形 $A B C D$ 摆放在一起，使三角板的直角顶点和正方形的顶点C始终重合，连 $A F$ ，取 $A F$ 的中点M， $E F$ 的中点N，连接 $M D 、 M N$ ．

(1)、若直角三角板 $E C F$ 和正方形 $A B C D$ 如图1摆放，点E、F分别在正方形的边 $C B$ 、 $C D$ 上．请判断 $M D$ 与 $M N$ 之间的数量关系，并加以证明；

(2)、若直角三角板 $E C F$ 和正方形 $A B C D$ 如图2摆放，点E、F分别在 $B C 、 D C$ 的延长线．其他条件不变，则（1）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

(3)、若 $A B = 3 ， C E = 2$ ，连接 $D N$ ．在摆放的过程中， $△ D M N$ 的面积存在最大值 $S_{1}$ 和最小值 $S_{2}$ ，请直接写出 $S_{1}$ 和 $S_{2}$ 的值．

查看试题解析

体温（℃）	35.8	36.1	36.2	36.3	36.4	36.5	36.6	36.8
人数（人）	3	4	8	8	10	8	2	2

分数	7分	8分	9分	10分
人数	11	0		8