广东省广州市南沙区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 在中,如果 , , 那么的度数是( )A、 B、 C、 D、无法确定3. 在函数中,当自变量时,函数值等于( )A、1 B、4 C、7 D、134. 某城市3月份某星期7天的最低气温如下(单位):16,20,18,16,18,18,17,这组数据的众数是( )A、16 B、17 C、18 D、205. 直角三角形的两条直角边长分别为2和3,那么它的斜边的长是( )A、或 B、4 C、 D、6. 一次函数中,y随着x的增大而减小,那么它的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,的对角线 , 相交于点 , 是等边三角形,且 , 那么的面积是( )
 A、 B、 C、 D、88. 如图,在平面直角坐标系中,点A和点B的坐标分别是: , . 那么线段的长度是( )
A、 B、 C、 D、88. 如图,在平面直角坐标系中,点A和点B的坐标分别是: , . 那么线段的长度是( ) A、 B、 C、5 D、9. 定义新运算“※”的运算法则为:当 , 时, . 例如: . 那么的值是( )A、8 B、48 C、 D、10. 如图,直线与x轴、y轴分别交于点A和点B,点C和点D分别是线段 , 的中点,点P为线段上的一动点,则值最小时点P的坐标是( )
A、 B、 C、5 D、9. 定义新运算“※”的运算法则为:当 , 时, . 例如: . 那么的值是( )A、8 B、48 C、 D、10. 如图,直线与x轴、y轴分别交于点A和点B,点C和点D分别是线段 , 的中点,点P为线段上的一动点,则值最小时点P的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若二次根式有意义,则a的取值范围是 .12. 直线与x轴的交点坐标是13. 在某校举办的队列比赛中,A班的成绩如下:
项目
着装
队形
精神风貌
成绩/分
90
95
95
若按着装占10%、队形占60%、精神风貌占30%计算参赛班级的综合成绩,则班的最后得分是分.
14. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.15. 如图,正比例函数和一次函数的图象相交于点 , 那么不等式的解集是 . 16. 如图①是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O的直角三角形演化而成的.如果图②中的 , 那么的长是 .
16. 如图①是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O的直角三角形演化而成的.如果图②中的 , 那么的长是 .
三、解答题
-
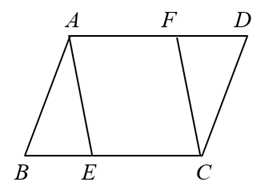
17. 计算: .18. 如图,在中,点E,点F分别是和的中点.求证: .
 19. 如图,在中,于D, , , , 求的长.
19. 如图,在中,于D, , , , 求的长. 20. 已知点在直线上.(1)、求b的值.(2)、若直线与y轴交于点B,求的面积.21. 为了进一步落实“双减”政策,某学校对本校初一学生“每天做家庭作业所用的大致时间(时间以整数记,单位:分钟)”做了抽样调查,并把调查所得到的所有数据(时间)进行整理,分成四个时间段,绘制成统计表和统计图(如下图).请结合统计表和统计图中提供的信息,回答下面的问题:
20. 已知点在直线上.(1)、求b的值.(2)、若直线与y轴交于点B,求的面积.21. 为了进一步落实“双减”政策,某学校对本校初一学生“每天做家庭作业所用的大致时间(时间以整数记,单位:分钟)”做了抽样调查,并把调查所得到的所有数据(时间)进行整理,分成四个时间段,绘制成统计表和统计图(如下图).请结合统计表和统计图中提供的信息,回答下面的问题:作业时间/分钟
频率
0.10
0.30
a
0.25
 (1)、本次抽样调查的样本容量是 , 统计表中a=;(2)、请把统计图补充完整,并在图中标明相应数据;(3)、这次调查得到的所有数据中位数落在了四个时间段中的段内.22. 一辆汽车和一辆摩托车分别从A、B两地前往同一个地方C城,它们距离A地的路程随着时间的变化的图象如图所示.
(1)、本次抽样调查的样本容量是 , 统计表中a=;(2)、请把统计图补充完整,并在图中标明相应数据;(3)、这次调查得到的所有数据中位数落在了四个时间段中的段内.22. 一辆汽车和一辆摩托车分别从A、B两地前往同一个地方C城,它们距离A地的路程随着时间的变化的图象如图所示.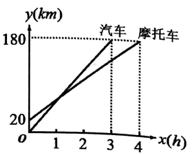 (1)、求摩托车整个过程中的平均速度.(2)、如果两车同时出发,汽车在某处与摩托车相遇,求此时两车距离A地的距离.(3)、如果摩托车到达C城后马上以原来的速度原路返回,求摩托车从B地出发5.5小时后与A地的距离.23. 在学习了算术平方根和二次根式等内容后,我们知道以下的结论:
(1)、求摩托车整个过程中的平均速度.(2)、如果两车同时出发,汽车在某处与摩托车相遇,求此时两车距离A地的距离.(3)、如果摩托车到达C城后马上以原来的速度原路返回,求摩托车从B地出发5.5小时后与A地的距离.23. 在学习了算术平方根和二次根式等内容后,我们知道以下的结论:结论①:若实数时,;结论②:对于任意实数a, .
请根据上面的结论,对下列问题进行探索:
(1)、若 , 化简: .(2)、若 , , 且 , 求的值.(3)、若有意义,化简 .24. 如图1,在正方形中,E是的中点. (1)、若 , 求的长.(2)、如图2,F是线段上的一点,且 , 求证:是直角三角形.(3)、如图3是一个正方体,棱长 , 的中点E处有一只蚂蚁,蚂蚁从处出发在正方体表面爬行,经过上某点P处后继续沿直线方向爬到正方体的顶点G处.当的值最小时,求的长.25. 如图,在四边形中, , , , , . 点P从A出发,以的速度向点D运动;点Q从C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动的时间为t秒.
(1)、若 , 求的长.(2)、如图2,F是线段上的一点,且 , 求证:是直角三角形.(3)、如图3是一个正方体,棱长 , 的中点E处有一只蚂蚁,蚂蚁从处出发在正方体表面爬行,经过上某点P处后继续沿直线方向爬到正方体的顶点G处.当的值最小时,求的长.25. 如图,在四边形中, , , , , . 点P从A出发,以的速度向点D运动;点Q从C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动的时间为t秒. (1)、设线段的长为 , 求y关于t的函数解析式及自变量t的取值范围.(2)、从运动开始,当时,求t的值.(3)、从运动开始,当时,求t的值.
(1)、设线段的长为 , 求y关于t的函数解析式及自变量t的取值范围.(2)、从运动开始,当时,求t的值.(3)、从运动开始,当时,求t的值.