广东省广州市黄埔区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 在实数范围内有意义,实数x的取值范围是( )A、 B、 C、 D、2. 某校劳动实践活动中,甲,乙两块试验田3次果蔬平均产量都是 , 方差分别是 , , 则这两块试验田3次果蔬产量较稳定的是( )A、甲 B、乙 C、甲和乙一样稳定 D、不能确定3. 下列根式是最简二次根式的是( )A、 B、 C、 D、4. 一次函数的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下面是某校八年级(2)班一组女生的体重(单位:):35,36,38,40,42,42,75.则这组数据的众数和中位数分别是( )A、40,42 B、42,40 C、42,44 D、40,386. 在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )A、测量对角线是否相互平分 B、测量两组对边是否分别相等 C、测量一组对角是否都为直角 D、测量四边形其中的三个角是否都为直角7. 一个直角三角形的模具,其中两边长分别为4cm、3cm,则第三条边长为( )A、5cm B、4cm C、cm D、5cm或cm8. 若直线y=kx+b经过第一、二、三象限,则函数y=bx﹣k的大致图象是( )A、
 B、
B、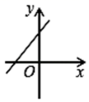 C、
C、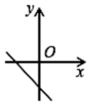 D、
D、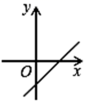 9. 如图,函数y=2x和y=ax+5的图象交于点A(m,3),则不等式2x<ax+5的解集是( )
9. 如图,函数y=2x和y=ax+5的图象交于点A(m,3),则不等式2x<ax+5的解集是( )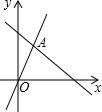 A、x< B、x<3 C、x> D、x>310. 下列命题:①若是整数,则正整数n的最小值是12;②“”与“”均一定成立;③“如果 , , (n是正整数)是一组勾股数,那么正整数a,b,c也是一组勾股数”的逆命题是真命题;④四条边相等的四边形是菱形,四个角相等的四边形是正方形,错误的有( )A、1个 B、2个 C、3个 D、4个
A、x< B、x<3 C、x> D、x>310. 下列命题:①若是整数,则正整数n的最小值是12;②“”与“”均一定成立;③“如果 , , (n是正整数)是一组勾股数,那么正整数a,b,c也是一组勾股数”的逆命题是真命题;④四条边相等的四边形是菱形,四个角相等的四边形是正方形,错误的有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算:①×= , ②= , ③= .12. 函数的图象与x轴的交点坐标是;y随x的增大而;当时,x的取值范围是 .13. 某校规定学生的学期体育成绩由三部分组成:体育课外活动占学期成绩的10%,理论测试占30%,体育技能测试占60%,一名同学上述三项成绩依次为90分,92分,73分,则该同学这学期的体育成绩为分.14. 已知 , , 求下列各式的值:(1)、;(2)、;(3)、 .15. 某车间的甲、乙两名工人分别同时生产同一种零件,他们一天生产零件的个数y(个)与生产时间t(小时)函数图象分别如图所示:
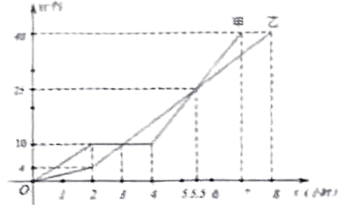 (1)、甲、乙两人中,(填写:“甲”/“乙”)先完成一天的生产任务.(2)、生产过程中,甲乙两人中(填写:“甲”/“乙”)因机器故障停止生产,停止生产了小时.(3)、当时,甲、乙生产的零件个数相等.16. 如图,四边形是菱形, , 是边上的动点,交边于点 . 当线段最短时, . 此时点到直线的距离是 .
(1)、甲、乙两人中,(填写:“甲”/“乙”)先完成一天的生产任务.(2)、生产过程中,甲乙两人中(填写:“甲”/“乙”)因机器故障停止生产,停止生产了小时.(3)、当时,甲、乙生产的零件个数相等.16. 如图,四边形是菱形, , 是边上的动点,交边于点 . 当线段最短时, . 此时点到直线的距离是 .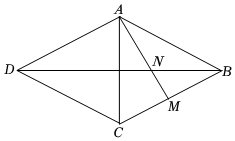
三、解答题
-
17. 计算: .18. 如图,在平面直角坐标系中,三个顶点的坐标分别为 , , .
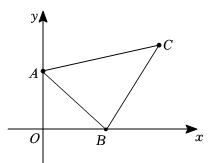 (1)、求A,B两点间距离.(2)、试说明是直角三角形.19. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
(1)、求A,B两点间距离.(2)、试说明是直角三角形.19. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
分别计算这些运动员成绩的平均数、中位数、众数(结果保留小数点后两位).
20. 已知变量y与x之间的函数关系如图所示,请用“待定系数法”求: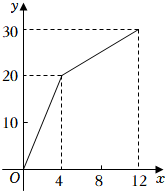 (1)、当时,y关于x的函数解析式.(2)、当时,y关于x的函数解析式.21. A,B两家商场为了吸引顾客,推出不同的优惠方案出售相同的某商品.A商场原售价是5元/千克,现按8折出售.B商场原售价是6元/千克,优惠方案为:10千克以内(含10千克)不优惠,超过10千克部分按5折出售.(1)、以x(单位:千克)表示商品重量,y(单位:元)表示售价,分别就两家商场的优惠方案写出y关于x的函数解析式;(2)、如何选择这两家商场去购买该商品更省钱?22. 如图,△ACB和△ECD都是等腰直角三角形, , 的顶点A在的斜边上,连接 .
(1)、当时,y关于x的函数解析式.(2)、当时,y关于x的函数解析式.21. A,B两家商场为了吸引顾客,推出不同的优惠方案出售相同的某商品.A商场原售价是5元/千克,现按8折出售.B商场原售价是6元/千克,优惠方案为:10千克以内(含10千克)不优惠,超过10千克部分按5折出售.(1)、以x(单位:千克)表示商品重量,y(单位:元)表示售价,分别就两家商场的优惠方案写出y关于x的函数解析式;(2)、如何选择这两家商场去购买该商品更省钱?22. 如图,△ACB和△ECD都是等腰直角三角形, , 的顶点A在的斜边上,连接 . (1)、求证: .(2)、若 , , 求的长.23. 如图,在四边形中,// , , , , , 点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始:
(1)、求证: .(2)、若 , , 求的长.23. 如图,在四边形中,// , , , , , 点P从点A出发,以的速度向点D运动;点Q从点C同时出发,以的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始: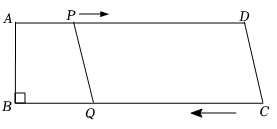 (1)、当运动 , 判断此时:四边形的形状,并证明.(2)、当时,求长.(3)、当时,需经过多少时间?
(1)、当运动 , 判断此时:四边形的形状,并证明.(2)、当时,求长.(3)、当时,需经过多少时间?