广东省广州市白云区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列函数中,是正比例函数的是( )A、 B、 C、 D、2. ( )A、-2.25 B、-1.5 C、1.5 D、2.253. 关于函数 , 的图象,下列说法正确的是( )A、这两个函数的图象均与y轴交于 B、这两个函数的图象均与x轴交于 C、这两个函数的图象均与x轴交于 D、这两个函数的图象均与y轴交于4. 如图,把一个长方形的纸片对折两次,然后剪下一个角,把剪下部分展开后,得到的图形是( )
 A、平行四边形 B、菱形 C、矩形 D、正方形5. 在一次青年歌手演唱比赛中,评分办法采用10位评委现场打分,每位选手的最后得分为去掉最低分、最高分后的平均数.已知10位评委给某位歌手的打分是9.5 9.5 9.3 9.8 9.4 8.8 9.6 9.5 9.2 9.6.则这位歌手的最后得分是( )A、9.45 B、9.44 C、9.43 D、9.426. 如图,一木杆在离地面4m的A处折断,木杆顶端落在离木杆底端3m的B处.则A木杆折断之前的长度为( )
A、平行四边形 B、菱形 C、矩形 D、正方形5. 在一次青年歌手演唱比赛中,评分办法采用10位评委现场打分,每位选手的最后得分为去掉最低分、最高分后的平均数.已知10位评委给某位歌手的打分是9.5 9.5 9.3 9.8 9.4 8.8 9.6 9.5 9.2 9.6.则这位歌手的最后得分是( )A、9.45 B、9.44 C、9.43 D、9.426. 如图,一木杆在离地面4m的A处折断,木杆顶端落在离木杆底端3m的B处.则A木杆折断之前的长度为( )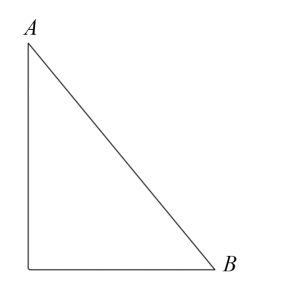 A、6m B、7m C、8m D、9m7. 一个三角形的三边长分别为 , , 2,则这个三角形是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形8. 已知一次函数的图象经过点 , , , 则( )A、 B、 C、 D、9. 下列各曲线中,表示y是x的函数的是( )A、
A、6m B、7m C、8m D、9m7. 一个三角形的三边长分别为 , , 2,则这个三角形是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形8. 已知一次函数的图象经过点 , , , 则( )A、 B、 C、 D、9. 下列各曲线中,表示y是x的函数的是( )A、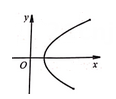 B、
B、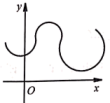 C、
C、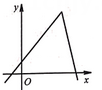 D、
D、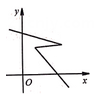 10. 下列命题的逆命题中,是假命题的是( )A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、对角线互相垂直的四边形是矩形 D、有一个角是直角的四边形是矩形
10. 下列命题的逆命题中,是假命题的是( )A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、对角线互相垂直的四边形是矩形 D、有一个角是直角的四边形是矩形二、填空题
-
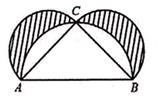
11. 比较大小:3.12. 在平面直角坐标系中,有两点和 , 则A,B两点间的距离为 .13. 如图,分别以等腰的边AB,AC,BC为直径画半圆,若 , 则阴影部分的面积为 .
 14. 把A,B两组数据分别画成下面的图1和图2,比较这两幅图,可以看出,组数据的方差较大,组数据的波动较小.
14. 把A,B两组数据分别画成下面的图1和图2,比较这两幅图,可以看出,组数据的方差较大,组数据的波动较小.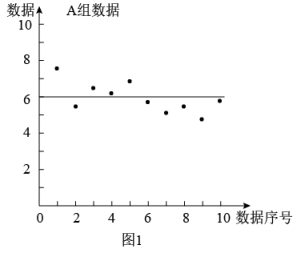
 15. 函数的图象,可以看作由直线向平移个单位长度而得到.16. 如图,在正方形ABCD中,点E是直线BC上一点, , 且EF交正方形外角的平分线CF于点F.下列说法正确的是 . (填序号)
15. 函数的图象,可以看作由直线向平移个单位长度而得到.16. 如图,在正方形ABCD中,点E是直线BC上一点, , 且EF交正方形外角的平分线CF于点F.下列说法正确的是 . (填序号)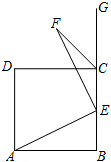
①若点E是BC的中点,则;
②若点E是BC边上的任意一点(中点除外),则;
③若点E是BC延长线上任意一点,则;
④若点E是BC反向延长线上任意一点,则 .
三、解答题
-
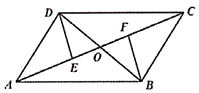
17. 计算: .18. 计算: .19. 如图,的对角线AC,BD相交于点O.已知E,F分别是OA,OC的三等分点,其中 , . 求证: .
 20. 当自变量x满足什么条件时,的函数值不小于的函数值?21.(1)、3k,4k,5k(k是正整数)是一组勾股数吗?如果是,请证明;如果不是,请说明理由;(2)、如果a,b,c是一组勾股数,那么ak,bk,ck(k是正整数)也是一组勾股数吗?如果是,请证明;如果不是,请说明理由.22. 下表是校女子排球队队员的年龄分布.
20. 当自变量x满足什么条件时,的函数值不小于的函数值?21.(1)、3k,4k,5k(k是正整数)是一组勾股数吗?如果是,请证明;如果不是,请说明理由;(2)、如果a,b,c是一组勾股数,那么ak,bk,ck(k是正整数)也是一组勾股数吗?如果是,请证明;如果不是,请说明理由.22. 下表是校女子排球队队员的年龄分布.年龄/岁
13
14
15
16
频数
1
4
5
2
(1)、该校女子排球队队员年龄的中位数是 , 众数是;(2)、求该校女子排球队队员的平均年龄约为多少岁?(结果保留到整数).23. 在数轴上分别作出表示和的点.(要求:用尺规作图,保留作图痕迹.不要求写作法.)24. 如图,一次函数的图象上A,B两点,点A在第一象限,点B在x轴上.点D在x轴正半轴上,点C的坐标为 , 四边形OADC为菱形.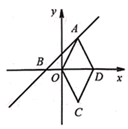 (1)、求k的值;(2)、求的面积;.(3)、设点P是直线AB上一动点,且 , 求点P的坐标.25. 在菱形ABCD中, , 点P是平面内一动点,以AP为边作等边 , 其中A,P,E按逆时针方向排列.
(1)、求k的值;(2)、求的面积;.(3)、设点P是直线AB上一动点,且 , 求点P的坐标.25. 在菱形ABCD中, , 点P是平面内一动点,以AP为边作等边 , 其中A,P,E按逆时针方向排列.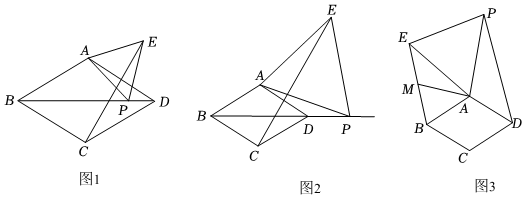 (1)、如图1,当点P在线段BD上,点E在菱形ABCD外部时,连接CE.求证:;(2)、观察图1,图2,请直接写出当点P在射线BD上运动时,点E的运动路径是什么?(3)、如图3,当在菱形ABCD外侧时,连接BE,DP,点M为BE的中点.请探索DP和AM之间有怎样数量关系?写出猜想,并证明.
(1)、如图1,当点P在线段BD上,点E在菱形ABCD外部时,连接CE.求证:;(2)、观察图1,图2,请直接写出当点P在射线BD上运动时,点E的运动路径是什么?(3)、如图3,当在菱形ABCD外侧时,连接BE,DP,点M为BE的中点.请探索DP和AM之间有怎样数量关系?写出猜想,并证明.