广东省佛山市南海区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $a < b$ ，下列各式中正确的是（）

A、 $a c^{2} < b c^{2}$ B、 $\frac{1}{a} > \frac{1}{b}$ C、 $- 3 a > - 3 b$ D、 $\frac{a}{4} > \frac{b}{4}$

查看试题解析
2. 如图汽车标志中不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值等于0，则 $x$ 的值为（）

A、 $x = \pm 2$ B、 $x = 2$ C、 $x = - 2$ D、 $x \neq - 2$

查看试题解析
4. 小李家装饰地面，已有正三角形形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则小李不应购买的地砖形状是（）

A、正方形 B、正六边形 C、正八边形 D、正十二边形

查看试题解析
5. 把 $a^{2} - 4 a$ 多项式分解因式，结果正确的是（）

A、 $a (a - 4)$ B、 $(a + 2) (a - 2)$ C、 $a (a + 2) (a - 2)$ D、 $(a - 2)^{2} - 4$

查看试题解析
6. 下列各式计算正确的是（）

A、 $\frac{a + b}{a + c} = \frac{b}{c}$ B、 $\frac{1 - a}{a - 2} = - \frac{a - 1}{a - 2}$ C、 ${(\frac{2 y}{x})}^{3} = \frac{6 y^{3}}{x^{3}}$ D、 $\frac{x^{6}}{x^{3}} = x^{2}$

查看试题解析
7. 用一条长为16cm的细绳首尾连接围成一个等腰三角形，若其中有一边的长为4cm，则该等腰三角形的腰长为（）

A、4cm B、6cm C、4cm或6cm D、4cm或8cm

查看试题解析
8. 在平面直角坐标系中，已知A（﹣2，3），B（2，1），将线段AB平移后，A点的坐标变为（﹣3，2），则点B的坐标变为（）

A、（﹣1，2） B、（1，0） C、（﹣1，0） D、（1，2）

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， CE垂直平分线段AD于E，且CD平分 $∠ B C E$ ， $A C = 8 c m$ ，则 $A B =$ （）．

A、10cm B、16cm C、24cm D、30cm

查看试题解析
10. 如图，在平行四边形ABCD中，E、F分别是边AB、CD的中点，BD分别交CE、AF于G、H，试判断下列结论：① $△ C B E ≌ △ A D F$ ；② $C G = A H$ ；③ $B G = \frac{1}{2} G D$ ；④ $S_{△ C B G} = 2 S_{△ F H D}$ ．其中正确的结论有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

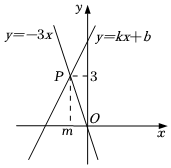
11. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是．

查看试题解析
12. 三个连续自然数的和小于13，这样的自然数有组．

查看试题解析
13. 分式方程 $\frac{2}{x - 2} = \frac{1}{x + 2}$ 的解是．

查看试题解析
14. 命题“等腰三角形的两个底角相等．”的逆命题是．

查看试题解析
15. 如图，在平面直角坐标系中，函数 $y = - 3 x$ 与 $y = k x + b (k > 0)$ 的图象交于点 $P (m ， 3)$ ，则不等式 $k x + b < - 3 x$ 的解集为．

查看试题解析
16. 如图，在平行四边形ABCD中， $A E ⊥ B C$ 于E， $A F ⊥ C D$ 于F，若 $A E = 2$ ， $A F = 3$ ，平行四边形ABCD的周长为20．则平行四边形ABCD的面积为．

查看试题解析
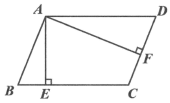17. 如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB， $∠ O A B = 90 °$ ，直角边AO在x轴上，且 $B O = 3$ ．将 $R t △ A O B$ 绕原点O顺时针旋转90°，并将旋转后的图形放大，使 $B_{1} O = 3 B O$ ，得到等腰直角三角形 $A_{1} O B_{1}$ ， ……，依此规律，得到等腰直角三角形 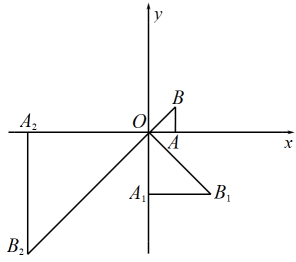$A_{2022} O B_{2022}$ 则点 $B_{2022}$ 的坐标为．

查看试题解析

三、解答题

18. 解不等式组 ${\begin{array}{l} 5 x + 4 \geq 2 (x - 1) \\ \frac{x}{3} > 1 - \frac{x - 3}{6} \end{array}$

查看试题解析
19. 先化简，再求值： $(\frac{4 x}{x - 2} - \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，在 $- 2$ 、0、1、2四个数中选一个合适的代入求值．

查看试题解析
20. 如图，锐角△ABC中，AB＝8，AC＝5．

(1)、请用尺规作图法，作BC的垂直平分线DE，垂足为E，交AB于点D（不要求写作法，保留作图痕迹）；

(2)、在（1）的条件下，连接CD，求△ACD周长．

查看试题解析
21. 如图，在边长为1的正方形组成的网格中建立直角坐标系， $△ A O B$ 的顶点均在格点上，点O为原点．

( 1 )将 $△ A O B$ 向下平移3个单位后得到 $△ A_{1} O_{1} B_{1}$ ，请在图中画出 $△ A_{1} O_{1} B_{1}$ ，其中，点 $A_{1}$ 的坐标为．

( 2 )将 $△ A O B$ 绕点O逆时针旋转90°后得到 $△ A_{2} O B_{2}$ ，请在图中画出 $△ A_{2} O B_{2}$ ，其中，点 $A_{2}$ 的坐标为．

( 3 )在（2）的旋转过程中，求线段OA扫过图形的面积．

查看试题解析
22. 如图，点B、E分别在AC，DF上，AF分别交BD、CE于点M、N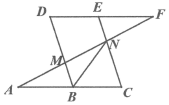， $∠ C = ∠ D$ ， $∠ B M A = ∠ E N F$ ．

(1)、求证：四边形BCED是平行四边形．

(2)、连接BN，若BN平分 $∠ D B C$ ， $D E = 5$ ，求CN的长．

查看试题解析
23. 某地区制订对区、镇两级的旧城镇旧村居改造三年计划．现某村计划对面积为 $9000 m^{2}$ 的旧村居进行改造，安排A、B两个公司完成．已知A公司每天能改造的面积是B公司的2倍，并且独立完成面积为 $600 m^{2}$ 旧村居的改造时，A公司比B公司队少用6天．

(1)、求A、B两公司每天能改造的面积分别是多少 $m^{2}$ ？

(2)、若每天需付给A公司的改造费用为0.8万元，B公司为0.3万元，要使这次的改造总费用不超过60万元，至多应安排A公司工作多少天？

查看试题解析
24. 如图1，在平面直角坐标系xOy中，有长方形OABC，其中点C坐标为 $(0 ， \sqrt{3})$ ， $∠ C A O = 30 °$ ，点D是边OC的中点，点P是射线CA上的一个动点，请回答下面的问题：

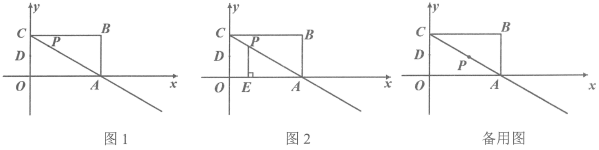(1)、若点P是线段AC的中点，直接写出 $P D =$ ．

(2)、如图2，过点P作 $P E ⊥ x$ 轴，垂足是点E，若以C、D、E、P为顶点的四边形是平行四边形，求出点P的坐标．

(3)、连接BP，若 $△ C P B$ 是等腰三角形，求CP的长度．

查看试题解析
25. 如图1， $△ A B C$ 为等边三角形，在AB、AC上分别取点E、D，使 $A E = A D$ ，连接DE．

(1)、求证： $△ A D E$ 是等边三角形．

(2)、点M、N分别是BE、CD的中点，连接MN，当 $△ A D E$ 绕A点旋转到如图2的位置时，求 $∠ A M N$ 的度数．

(3)、在（2）的条件下，若 $∠ C A D = 30 °$ ， $A C = 14$ ， $D E = 4 \sqrt{3}$ ，求AN的长．

查看试题解析