广东省佛山市禅城区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手,开展安全教育,下列安全图标是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 要使分式 有意义,则x应满足的条件是( )A、 B、 C、 D、3. 下列由左边到右边的变形,是因式分解的是( )A、 B、 C、 D、4. 已知:中,D、E、F分别是边、、的中点,则四边形的周长等于( )
2. 要使分式 有意义,则x应满足的条件是( )A、 B、 C、 D、3. 下列由左边到右边的变形,是因式分解的是( )A、 B、 C、 D、4. 已知:中,D、E、F分别是边、、的中点,则四边形的周长等于( ) A、 B、 C、 D、的周长5. 如果分式的值等于0,那么m的值为( )A、不存在 B、 C、4 D、-46. 下列条件中,不能判定两个直角三角形全等的是( )A、一个锐角和斜边对应相等 B、两条直角边对应相等 C、两个锐角对应相等 D、斜边和一条直角边对应相等7. 过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )A、5 B、6 C、7 D、88. 若 , 且 , 则的取值范围是( )A、 B、 C、 D、9. 如图,在 中, 分别是 的中点,点F在 延长线上,添加一个条件使四边形 为平行四边形,则这个条件是( )
A、 B、 C、 D、的周长5. 如果分式的值等于0,那么m的值为( )A、不存在 B、 C、4 D、-46. 下列条件中,不能判定两个直角三角形全等的是( )A、一个锐角和斜边对应相等 B、两条直角边对应相等 C、两个锐角对应相等 D、斜边和一条直角边对应相等7. 过一个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )A、5 B、6 C、7 D、88. 若 , 且 , 则的取值范围是( )A、 B、 C、 D、9. 如图,在 中, 分别是 的中点,点F在 延长线上,添加一个条件使四边形 为平行四边形,则这个条件是( )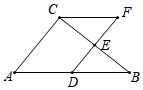 A、 B、 C、 D、10. 某厂计划加工180万个医用口罩,第一周按原计划的速度生产,一周后以原来速度的1.5倍生产,结果比原计划提前一周完成任务若设原计划每周生产x万个口罩,则可列方程为( )A、 B、 C、 D、11. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( )
A、 B、 C、 D、10. 某厂计划加工180万个医用口罩,第一周按原计划的速度生产,一周后以原来速度的1.5倍生产,结果比原计划提前一周完成任务若设原计划每周生产x万个口罩,则可列方程为( )A、 B、 C、 D、11. 用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做平面镶嵌问题.如图,利用相同边长的正三角形可以进行平面镶嵌.请问下列图形或图形组合无法进行平面镶嵌的是( ) A、全等三角形 B、边长相等的正方形 C、边长相等的正三角形 D、边长相等的正五边形12. 如图,在平行四边形中,以点A为圆心,长为半径画弧交于点F,再分别以点B、F为圆心,大于的相同长为半径画弧,两弧交于点P,连接并延长交于点E,连接 . 根据以上尺规作图的过程,小明得到下列结论:①平分 ②是等边三角形 ③ ④ , 其中,结论正确的有( )个
A、全等三角形 B、边长相等的正方形 C、边长相等的正三角形 D、边长相等的正五边形12. 如图,在平行四边形中,以点A为圆心,长为半径画弧交于点F,再分别以点B、F为圆心,大于的相同长为半径画弧,两弧交于点P,连接并延长交于点E,连接 . 根据以上尺规作图的过程,小明得到下列结论:①平分 ②是等边三角形 ③ ④ , 其中,结论正确的有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 已知等腰三角形的顶角是 , 则这个等腰三角形的底角是 .14. 在平行四边形中, , , , 则平行四边形的面积等于 .
 15. 分解因式: .16. 解方程的结果是 .17. 函数和的图象相交于点 , 则关于x的不等式的解集为 .
15. 分解因式: .16. 解方程的结果是 .17. 函数和的图象相交于点 , 则关于x的不等式的解集为 .三、解答题
-
18. 三个数 , , 3在数轴上从左到右依次排列,求a的取值范围.19. 先化简: ,再请从-2、-1、0、1中选一个你认为合适的数作为x的值,代入求值.20. 已知:如图,在中,、分别是、边上的高,它们相交于点F,且 . 求证:是等腰三角形.
 21. 如图,方格纸中每个小正方形的边长都是1个单位长度,的三个顶点分别为 , , . 按要求画出图形,并回答问题:
21. 如图,方格纸中每个小正方形的边长都是1个单位长度,的三个顶点分别为 , , . 按要求画出图形,并回答问题: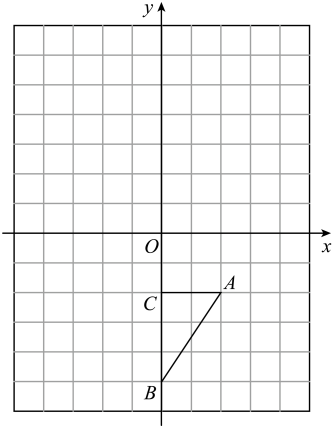
( 1 )画 , 使它与关于点成中心对称;则的坐标为 ▲ .
( 2 )平移 , 使点的对应点的坐标为 , 画出平移后对应的 , 则的坐标为 ▲ .
( 3 )若将绕某一点旋转可得到 , 则旋转中心的坐标为 ▲ .
22. 如图,在平行四边形中, , 将纸片沿对角线对折,边与边交于点E,此时,恰为等边三角形. (1)、求证: .(2)、求重叠部分的面积.(3)、连接 , 证明:四边形为平行四边形.23. 2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.(1)、求该商家第一次购进冰墩墩多少个?(2)、若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?24. 如图,在平面直角坐标系中,已知直线是一次函数的图像,直线是一次函数的图象,点是两直线的交点,点、、、分别是两条直线与坐标轴的交点.
(1)、求证: .(2)、求重叠部分的面积.(3)、连接 , 证明:四边形为平行四边形.23. 2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.(1)、求该商家第一次购进冰墩墩多少个?(2)、若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?24. 如图,在平面直角坐标系中,已知直线是一次函数的图像,直线是一次函数的图象,点是两直线的交点,点、、、分别是两条直线与坐标轴的交点. (1)、用m、n分别表示点A、B、P的坐标;(2)、若四边形的面积是 , 且 , 试求点的坐标,并求出直线与的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
(1)、用m、n分别表示点A、B、P的坐标;(2)、若四边形的面积是 , 且 , 试求点的坐标,并求出直线与的函数表达式;(3)、在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.