天津市南开区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 二次根式有意义的条件是( )A、 B、 C、 D、2. 下列各曲线中表示y是x的函数的是( )A、
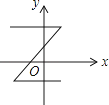 B、
B、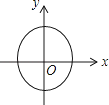 C、
C、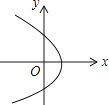 D、
D、 3. 如图,已知 ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点C的坐标为( )
3. 如图,已知 ABCD的两条对角线AC与BD交于平面直角坐标系的原点,点A的坐标为(-2,3),则点C的坐标为( )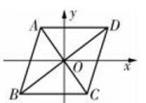 A、(-3,2) B、(-2,-3) C、(3,-2) D、(2,-3)4. 已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是A、-2 B、-1 C、0 D、25. 如图,直线l上有三个正方形,若a,c的面积分别为5和11,则b的面积为( )
A、(-3,2) B、(-2,-3) C、(3,-2) D、(2,-3)4. 已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是A、-2 B、-1 C、0 D、25. 如图,直线l上有三个正方形,若a,c的面积分别为5和11,则b的面积为( ) A、4 B、6 C、16 D、556. 将直线向右平移2个单位所得的直线的解析式是( )A、 B、 C、 D、7. 下列条件中,不能判断一个三角形是直角三角形的是( )A、三个角的比是 B、三条边 , , 满足关系 C、三条边的比是 D、三边长分别为1,2,8. 2022年北京-张家口举办了冬季奥运会,很多学校也开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差
A、4 B、6 C、16 D、556. 将直线向右平移2个单位所得的直线的解析式是( )A、 B、 C、 D、7. 下列条件中,不能判断一个三角形是直角三角形的是( )A、三个角的比是 B、三条边 , , 满足关系 C、三条边的比是 D、三边长分别为1,2,8. 2022年北京-张家口举办了冬季奥运会,很多学校也开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差队员1
队员2
队员3
队员4
平均数(秒)
51
50
51
50
方差(秒2)
3.5
3.5
14.5
14.5
据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A、队员1 B、队员2 C、队员3 D、队员49. 如图,在菱形中, , , 则菱形边上的高的长是( )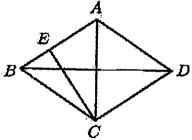 A、2.4 B、4.8 C、10 D、9.610. 一次函数与的图象如图,则下列结论:①;②;③当时, , 其中正确的结论有( )
A、2.4 B、4.8 C、10 D、9.610. 一次函数与的图象如图,则下列结论:①;②;③当时, , 其中正确的结论有( ) A、0个 B、1个 C、2个 D、3个11. 如图,在矩形中, , 点是边上靠近点的三等分点,动点从点出发,沿路径运动,则的面积与点经过的路径长之间的函数关系用图象表示大致是( )
A、0个 B、1个 C、2个 D、3个11. 如图,在矩形中, , 点是边上靠近点的三等分点,动点从点出发,沿路径运动,则的面积与点经过的路径长之间的函数关系用图象表示大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,在平面直角坐标系中, , 两点坐标分别为 , , 为线段上的一动点,以 , 为边构造平行四边形 , 则使对角线值最小的点的坐标为( )
12. 如图,在平面直角坐标系中, , 两点坐标分别为 , , 为线段上的一动点,以 , 为边构造平行四边形 , 则使对角线值最小的点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 化简:= .
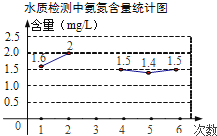
14.为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是mg/L.
 15. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处离远处竹子的距离为3尺,则原处还有竹子尺.(请直接写出答案,注:1丈=10尺.)
15. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处离远处竹子的距离为3尺,则原处还有竹子尺.(请直接写出答案,注:1丈=10尺.) 16. 如图,将一张矩形纸片ABCD沿EF折叠后,点C落在AB边上的点G处,点D落在点H处.若∠1=62°,则图中∠BEG的度数为.
16. 如图,将一张矩形纸片ABCD沿EF折叠后,点C落在AB边上的点G处,点D落在点H处.若∠1=62°,则图中∠BEG的度数为. 17. 若函数y=(m+3)x2m+1+4x﹣2(x≠0)是关于x的一次函数,m .18. 如图,已知正方形的边长为8,点 , 分别在 , 上, , 与相交于点 , 点为的中点,连接 , 则的长为 .
17. 若函数y=(m+3)x2m+1+4x﹣2(x≠0)是关于x的一次函数,m .18. 如图,已知正方形的边长为8,点 , 分别在 , 上, , 与相交于点 , 点为的中点,连接 , 则的长为 .
三、解答题
-
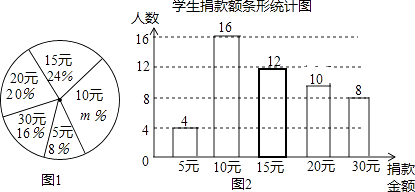
19. 计算(1)、(2)、20. 某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
 (1)、本次接受随机抽样调查的学生人数为 , 图①中m的值是;(2)、求本次你调查获取的样本数据的平均数、众数和中位数;(3)、根据样本数据,估计该校本次活动捐款金额为10元的学生人数.21. 如图,等边的边长是2, , 分别为 , 的中点,延长至点 , 使 , 连接和 .
(1)、本次接受随机抽样调查的学生人数为 , 图①中m的值是;(2)、求本次你调查获取的样本数据的平均数、众数和中位数;(3)、根据样本数据,估计该校本次活动捐款金额为10元的学生人数.21. 如图,等边的边长是2, , 分别为 , 的中点,延长至点 , 使 , 连接和 . (1)、求证:四边形为平行四边形;(2)、求的长.22. 如图,点是菱形对角线的交点, , 连接 .
(1)、求证:四边形为平行四边形;(2)、求的长.22. 如图,点是菱形对角线的交点, , 连接 . (1)、求证:;(2)、如果 , , 求四边形的周长.23. 工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为(小时),甲组加工零件的数量为(个),乙组加工零件的数量为(个),其函数图象如图所示:
(1)、求证:;(2)、如果 , , 求四边形的周长.23. 工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为(小时),甲组加工零件的数量为(个),乙组加工零件的数量为(个),其函数图象如图所示: (1)、填空:
(1)、填空:①;
②甲组工人每小时加工零件个;
③乙组工人每小时加工零件个;
④甲组加工小时的时候,甲、乙两组加工零件的总数为480个.
(2)、直接写出 , 与之间的函数关系式.24. 如图,在平面直角坐标系中,为坐标原点,矩形的顶点 , , 将矩形的一个角沿直线折叠,使得点落在对角线上的点处,折痕与轴交于点 .
 (1)、线段的长度为;(2)、求线段的长,以及直线所对应的函数表达式;(3)、若点为该平面内一点,且使得 , 直接写出满足条件的直线的解析式.
(1)、线段的长度为;(2)、求线段的长,以及直线所对应的函数表达式;(3)、若点为该平面内一点,且使得 , 直接写出满足条件的直线的解析式.