天津市河西区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{8}$ 的结果为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $3 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
2. 下列倡导节约的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 正方形的周长y是边长x的函数，则下列表示正方形周长y与边长x之间的函数关系正确的是（）

A、 $y = 2 x (x > 0)$ B、 $y = 4 x (x > 0)$ C、y=x²(x＞0) D、 $y = 4 x^{2} (x > 0)$

查看试题解析
4. 如图，网格中的小正方形边长均为1， $△ A B C$ 的三个顶点均在格点上，则AC的长度为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $\sqrt{5}$ D、25

查看试题解析
5. 一次函数 $y = 2 x + 2$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 当 $x = \sqrt{3}$ 时，代数式 $x^{2} + 2 x + 2$ 的值为（）

A、14 B、17 C、 $5 + 3 \sqrt{3}$ D、 $5 + 2 \sqrt{3}$

查看试题解析
7. 直线 $y = 2 x$ 与直线 $y = - x + 5$ 的交点为（）

A、 $(5 ， 10)$ B、 $(\frac{5}{3} ， \frac{10}{3})$ C、 $(4 ， 8)$ D、 $(\frac{4}{3} ， \frac{7}{3})$

查看试题解析
8. 有五根小木棒，其长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，其中正确的是（）

A、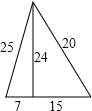 B、 C、 D、

查看试题解析
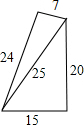9. 如图，点E，F，P，Q分别是正方形ABCD的四条边上的点，并且 $A F = B P = C Q = D E$ ，则下列结论不一定正确的是（）

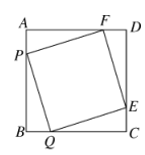A、 $∠ A F P = ∠ B P Q$ B、 $E F ∥ Q P$ C、四边形EFPQ是正方形 D、四边形PQEF的面积是四边形ABCD面积的一半

查看试题解析
10. 某超市出售一商品，有如下四种在原标价基础上调价的方案，其中调价后售价最低的是（）

A、先打九五折，再打九五折 B、先提价 $50 %$ ，再打六折 C、先提价 $30 %$ ，再降价 $30 %$ D、先提价 $25 %$ ，再降价 $25 %$

查看试题解析

二、填空题

11. 一个正方形的面积是50，则边长为．

查看试题解析
12. 计算（ $\sqrt{3} + 1$ ）（ $\sqrt{3} - 1$ ）的结果等于．

查看试题解析
13. 在一个等腰直角三角形中，如果斜边长为2，那么直角边的长为．

查看试题解析
14. 若一次函数 $y = k x + b$ （b为常数）的图像过点 $(1 ， 4)$ ，且与 $y = - 2 x$ 的图象平行，则这个一次函数的解析式为．

查看试题解析
15. 如图，平行四边形ABCO中的顶点O，A，C的坐标分别为 $(0 ， 0)$ ， $(2 ， 3)$ ， $(2 \sqrt{5} ， 0)$ ，则顶点B的坐标为．

查看试题解析
16. 已知正方形ABCD的边长为1，点E，F分别是边BC，CD上的两个动点，且满足 $B E = C F$ ，连接AE，AF，则 $A E + A F$ 的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\sqrt{7} - 1)}^{2}$

(2)、 $(\sqrt{2} + 1) (\sqrt{3} + \sqrt{2})$

查看试题解析
18. 下图是自动测温仪记录的图象，它反映了天津的春季某天气温T如何随时间t的变化而变化．

(1)、从这个函数图象可知：这一天中最低气温约为℃，最高气温约为℃．

(2)、从4时至14时气温随时间变化呈上升状态，请你指出气温随时间变化呈下降状态的时间段．

查看试题解析
19. 如图，将平面直角坐标系放在所示的网格中，每个小正方形的边长都为1， $△ A B C$ 的顶点都在格点上， $A (2 ， 2)$ ．

(1)、写出 $△ A B C$ 另两个顶点的坐标；

(2)、求此三角形的周长；

(3)、 $△ A B C$ 的面积为．

查看试题解析
20. 如图，菱形ABCD的边长为2， $∠ B C D = 120 °$ ，对角线AC，BD相交于点O，又有E，F分别为AB，AD的中点，连接EF．

(1)、求对角线AC的长；

(2)、求EF的长．

查看试题解析
21. 如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至点G，使EG＝AE，连接CG．

(1)、求证：△ABE≌△CDF；

(2)、当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．

查看试题解析
22. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

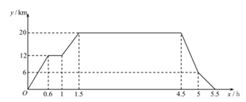
已知学校、书店、陈列馆依次在同一条直线上，书店离学校12km，陈列馆离学校20km．李华从学校出发，匀速骑行0.6h到达书店；在书店停留0.4h后，匀速骑行0.5h到达陈列馆；在陈列馆参观学习一段时间，然后回学校；回学校途中，匀速骑行0.5h后减速，继续匀速骑行回到学校．给出的图像反映了这个过程中李华离学校的距离ykm与离开学校的时间xh之间的对应关系．

请根据相关信息，解答下列问题：

(1)、填表：
离开学校的时间/h
0.1
0.5
0.8
1
3
离学校的距离/km
2
12

(2)、填空：
①李华在陈列馆参观学习的时间为h；

②李华从陈列馆回学校途中，减速前的骑行速度为km/h．

(3)、当 $0 \leq x \leq 1.5$ 时，请直接写出y关于x的函数解析式．

查看试题解析
23. 如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE，折叠该纸片，使点A恰好落在AE上的G处，得到折痕BF，与AD交于点F．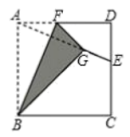

(1)、当E是CD的中点时，求AF的长；

(2)、若 $D E = 5$ ，求GE的长．

查看试题解析

离开学校的时间/h	0.1	0.5	0.8	1	3
离学校的距离/km	2			12