上海市徐汇区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数y=3（x﹣1）在y轴上的截距是（）

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
2. 下列方程中，有实数解的是（）

A、 $x^{2} + 1 = 0$ B、 $\sqrt{x - 2} - 3 = 0$ C、 $\frac{x + 1}{x^{2} - 1} = 0$ D、 $\sqrt{x - 2} + \sqrt{x} = 0$

查看试题解析
3. 如果关于反比例函数 $y = \frac{k}{x}$ （k是常数， $k \neq 0$ ），在每一个象限内，y随x的增大而减小，那么一次函数 $y = k x - 2$ 的图像一定经过（）

A、第一、二、三象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、四象限

查看试题解析
4. 如图，平行四边形ABCD的对角线AC和BD交于点O，下列选项中错误的是（）

A、 $\vec{A D} = \vec{B C}$ B、 $\vec{O A} + \vec{O C} = 0$ C、 $| \vec{O B} | = | \vec{O D} |$ D、 $| \vec{A B} | = | \vec{C D} |$

查看试题解析
5. 如图，函数 $y = k x + b$ 的图像与x轴、y轴分别相交于点 $A (0 ， 2)$ 和点 $B (4 ， 0)$ ，则关于x的不等式 $k x + b \geq 2$ 的解集为（）

A、 $x \leq 0$ B、 $x \leq 4$ C、 $x \geq 0$ D、 $x \geq 4$

查看试题解析
6. 下列事件中，必然事件是（）

A、经过有交通信号灯的路口，恰好遇到红灯 B、打开电视，正在播报新闻 C、抛掷两枚正方体骰子点数和等于13 D、任意画一个五边形，其外角和为360°

查看试题解析

二、填空题

7. 方程 $2 x^{3} - 16 = 0$ 的解是．

查看试题解析
8. 方程 $(x + 2) (x - 3) = 0$ 的解是．

查看试题解析
9. 如果将一次函数 $y = y = 5 x - 2$ 的图象沿y轴向上平移4个单位，那么平移后所得图象的函数解析式为．

查看试题解析
10. 用换元法解分式方程 $\frac{x^{2} + 1}{x} + \frac{2 x}{x^{2} + 1} = 3$ 时，如果设 $\frac{x}{x^{2} + 1} = y$ ，那么原方程可以化为关于y的整式方程是．

查看试题解析
11. 如果购买荔枝所付金额y（元）与购买数量x（千克）之间的函数图象由线段OA与射线AB组成（如图所示），那么购买3千克荔枝需要付元．

查看试题解析
12. 正五边形的内角和等于度.

查看试题解析
13. 如图， $△ A B C$ 中， $A B = A C = 5$ ， $B C = 4$ ， D、E分别是边AB、AC的中点，那么四边形DBCE的周长为．

查看试题解析
14. 我们知道，四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D'处，则点C的对应点C'的坐标为．

查看试题解析
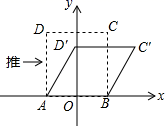15. 如图，菱形ABCD中，如果 $A B = 3$ ， $B D = 2$ ，那么菱形ABCD的面积为．

查看试题解析
16. 如图，将矩形ABCD的边BC延长至点E，使 $C E = B D$ ，联结AE交对角线BD于点F，交边CD于点G，如果 $∠ A D B = 38 °$ ，那么 $∠ E$ 的大小为．

查看试题解析
17. 如图，在梯形ABCD中， $A D ∥ B C$ ， $∠ B = 70 °$ ， $∠ C = 40 °$ ， $D E ∥ A B$ 交BC于点E．如果 $A D = 5$ cm， $B C = 12$ cm，那么CD的长是cm．

查看试题解析
18. 定义：如果一个凸四边形的一条对角线把四边形分成两个等腰三角形，那么称这个凸四边形为“等腰四边形”，把这条对角线称为“界线”。已知在“等腰四边形”ABCD中，AB=BC=AD，∠BAD=90°，且AC为“界线”，则∠BCD的度数为

查看试题解析

三、解答题

19. 解方程组 ${\begin{array}{l} x^{2} - 4 y^{2} = 0 \\ x^{2} + 6 x y + 9 y^{2} = 16 \end{array}$

查看试题解析
20. 解方程： $2 \sqrt{x + 6} + 2 = x$ ．

查看试题解析
21. 如图，已知点E是□ABCD的边BA延长线上一点，且 $A E = A B$ ．

(1)、写出 $\vec{D C}$ 所有的相反向量：；

(2)、计算： $\vec{A B} + \vec{A D} =$ ， $\vec{A D} - \vec{A E} =$ ；

(3)、求作： $\vec{D B} - \vec{E C}$ （要求写明结论）．

查看试题解析
22. 国宝大熊猫作为体育盛会的吉祥物见证了祖国的日益强大．从1990年北京亚运会的“盼盼”，到2008年北京奥运会的“福娃晶晶”，再到北京冬奥会的“冰墩墩”．现在将4张卡片（如图，分别记为A、B、C、D）背面朝上洗匀，这些卡片除图案外其余均相同．

(1)、小明从中随机抽取1张，抽到冰墩墩的概率为；

(2)、小明从中随机抽取2张，抽取规则为：先随机抽取1张不放回，再随机抽取1张．请利用树状图或列表法求出小明抽取的2张卡片都是冰墩墩的概率．

查看试题解析
23. 激光电视的光源是激光，它运用反射成像原理，屏幕不通电无辐射，降低了对消费者眼睛的伤害．某电器商行销售的某款激光电视去年销售总额为800万元，由于技术革新和成本降低，今年这款激光电视每台销售价比去年降低4000元，若要保持销售总额不变，今年这款激光电视的销售量要比去年多100台，今年这款激光电视每台的售价是多少元？

查看试题解析
24. 如图，正方形ABCD中，点E、F分别是边AD、CD上的点，BE平分 $∠ A E F$ ．

(1)、求证：BF平分 $∠ E F C$ ；

(2)、如果 $D F = 3$ ， $F C = 1$ ，求AE的长．

查看试题解析
25. 已知：如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = \frac{1}{2} x + 4$ 的图像与y轴交于点A，与反比例函数 $y = \frac{m}{x} (x > 0)$ 的图像交于点 $B (a ， 5)$ ．点C为函数 $y = \frac{1}{2} x + 4$ 的图像上一点，过点C作 $C D ∥ y$ 轴，交反比例函数 $y = \frac{m}{x}$ 的图像于点D．

(1)、求反比例函数 $y = \frac{m}{x}$ 的解析式；

(2)、如果 $B C = A B$ ，求点C的坐标；

(3)、如果 $B C = B D$ ，求点D的坐标．

查看试题解析
26. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $A B = 10$ ，点D是AB上的动点， $D E ∥ B C$ 交AC于点E， $D F ⊥ A B$ 分别交射线BC、射线AC于点F、G，联结EF．

(1)、如图1，如果点G恰好平分EC，判断四边形DEFC的形状并证明；

(2)、如图2，当点F在线段BC的延长线上时，设AD的长为x，梯形DBFE的面积为y，直接写出y关于x的函数关系及其定义域；

(3)、当 $E F = D B$ 时，求 $A D$ 的长．

查看试题解析