山西省晋中市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 将多项式 $m^{2} - m$ 分解因式，结果正确的是（）

A、 $m (m - 1)$ B、 $(m + 1) (m - 1)$ C、 $m (m + 1) (m - 1)$ D、 $- m (m - 1)$

查看试题解析
2. 2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若 $m > n$ ，则下列不等式不一定成立的是（）

A、 $m + 5 > n + 5$ B、 $- 3 m < - 3 n$ C、 $\frac{m}{2} > \frac{n}{2}$ D、 $m^{2} > n^{2}$

查看试题解析
4. 木工师傅将一个含45度角的三角尺和一个重锤如图放置，就能检查一根横梁是否水平，能解释这一现象的数学知识是（）

A、垂线段最短 B、等腰三角形的“三线合一” C、角平分线的性质定理 D、线段垂直平分线的性质定理

查看试题解析
5. 下列式子从左到右变形错误的是（）

A、 $\frac{m + 1}{n + 1} = \frac{m}{n}$ B、 $\frac{1 - m}{n} = - \frac{m - 1}{n}$ C、 $\frac{- 3 m}{- 3 n} = \frac{m}{n}$ D、 $\frac{1 - m}{m^{2} - 1} = - \frac{1}{m + 1}$

查看试题解析
6. 在复习平行四边形的判定方法时，某同学进行了画图探究，其作法和图形如下：①如图1，作线段AC的垂直平分线，交AC于点O；②如图2，过点O作一条直线l（不过点A，C）再以点O为圆心，任意长为半径作弧，交直线l于点B，D，连接AB，BC，CD，AD．根据以上作法，不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（）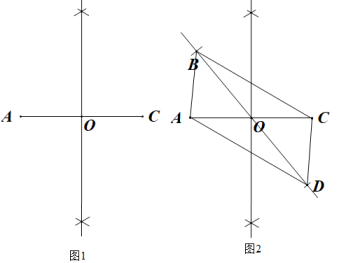

A、对角线互相平分的四边形是平行四边形 B、两组对边分别平行的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形

查看试题解析
7. 如图1 ，应县木塔位于山西省朔州市应县县城，是我国现存最古老最高大的纯木结构楼阁式建筑．经测量木塔建造在约四米之高的台基上，台基底层设计呈正多边形．如图2是台基底层正多边形的部分示意图，其外角为45°，则该正多边形是（）

A、正五边形 B、正六边形 C、正七边形 D、正八边形

查看试题解析
8. 抗击“新冠肺炎”疫情期间，某呼吸机厂接到一批生产150台呼吸机的订单，计划每天生产呼吸机a台，为了尽快完成任务，改进技术后实际提前2天完成任务，则实际生产这批呼吸机的天数为（）

A、 $\frac{150}{a - 2}$ B、 $\frac{150}{a + 2}$ C、 $\frac{150}{a} - 2$ D、 $\frac{150}{a} + 2$

查看试题解析
9. 如图，△ABC中，边AC，AB的垂直平分线相交于点D，若 $∠ C A D = 32 °$ ， $∠ A B D = 28 °$ ，则 $∠ B C D$ 的大小是（）

A、28° B、30° C、32° D、60°

查看试题解析
10. 如图，一次函，y＝﹣x－2，与 $y = k x + b$ 的图象交于点 $P (2 ， n)$ ，则关于x的不等式 $k x + b < - x - 2$ 的解集为（）

A、 $x < - 4$ B、 $x > 2$ C、 $x < 2$ D、 $0 < x < 2$

查看试题解析

二、填空题

11. 化简 $\frac{1}{a} \div \frac{1}{a^{2} - a}$ 的结果是．

查看试题解析
12. 如图，一个小孩坐在秋千上，秋千绕点O旋转了86°，小孩的位置也从A点运动到了 $A^{'}$ 点，则 $∠ O A A^{'} =$ 度．

查看试题解析
13. 如图1是某超市自动扶梯，如图2是其示意图，大厅两层之间的距离 $h = 6$ ，自动扶梯的倾斜角为30°．若自动扶梯运行速度 $v = 0.5$ 米/秒，则顾客乘自动扶梯上一层楼的时间为秒．

查看试题解析
14. 随着第24届冬季奥林匹克运动会在北京召开，全国掀起了冰雪运动的热潮．某校组织了关于冬奥知识竞答活动，一共有20道题．评分标准是：对1题给5分，错1题扣2分，不答题不给分也不扣分．在这次竞答中，敏敏有2道题未答，她要被评为优秀（总分80分或80分以上）至少要答对道题．

查看试题解析
15. 如图，在平行四边形ABCD中， $A D = 5$ ， $∠ D$ 是锐角， $C E ⊥ A D$ 于点E， $C E = 2 \sqrt{14}$ ， F是CD的中点，连接BF，EF．若 $∠ E F B = 90 °$ ，则DE的长为．

查看试题解析

三、解答题

16. 计算

(1)、解不等式组： ${\begin{array}{l} 1 - x < 2 \\ 6 - \frac{3}{2} x \geq 0 \end{array}$ ，并将其解集在数轴上表示出来；

(2)、解分式方程： $\frac{3 x}{x - 1} - 5 = \frac{x}{2 x - 2}$ ．

查看试题解析
17. 学完分式运算后，王老师出了一道化简题： $\frac{a + 1}{a - 1} + \frac{a + 1}{1 - a^{2}}$ ，请仔细阅读下面两位同学的解题过程并完成相应的任务：

(1)、任务一：老师判断上述两位同学的解法都错误，请你分别写出他们错误的原因，小明：，小花：；

(2)、任务二：请你写出正确的化简过程．

查看试题解析
18. 下列三幅图中的网格均由边长为1的小正方形组成，图1是三国时期吴国的数学家赵爽所绘制的“弦图”，它由四个形状、大小完全相同的直角三角形组成，赵爽利用这“弦图”对勾股定理作出了证明，是中国古代数学的一项重要成就，请根据下列要求解答问题．

(1)、图1中“弦图”的四个直角三角形组成的图形（阴影部分）是（填“轴”或“中心”）对称图形；

(2)、将“弦图”中的一个直角三角形作为基本图形，通过你所学过的图形变换知识，按下列要求画图：
①在图2中画出Rt△ABC向右平移4格后得到的△DEF；
②在图3中画出Rt△ABC绕点C顺时针旋转90°后得到的 $△ A^{'} B^{'} C$ ．

查看试题解析
19. 阅读下列材料：
小颖同学对多项式 $(x^{2} - 6 x + 3) (x^{2} - 6 x + 15) + 36$ 进行因式分解的过程中发现，如果把 $x^{2} - 6 x$ 看成一个整体，用一个新的字母代替，此多项式就可以运用公式法进行因式分解，以下是她的做法．

解：设 $x^{2} - 6 x = y$ ，

原式 $= (y + 3) (y + 15) + 36$

$= y^{2} + 18 y + 81$

$= {(y + 9)}^{2}$

$= {(x^{2} - 6 x + 9)}^{2}$

(1)、小颖同学进行因式分解时，所得到的最后结果是否分解彻底？（填“是”或“否”）；如果否，直接写出因式分解最后的结果；

(2)、请你模仿以上方法尝试对多项式 $(x^{2} - 2 x) (x^{2} - 2 x + 2) + 1$ 进行因式分解．

查看试题解析
20. 如图，已知BD是△ABC的角平分线，点E，F分别在边AB，BC上，且 $B E = C F$ ， $E D ∥ B C$ ．

(1)、求证：四边形EFCD是平行四边形；

(2)、若 $∠ A B C = 60 °$ ， $∠ A D B = 100 °$ ，求 $∠ A E F$ 的度数．

查看试题解析
21. 随着国内快递业务量的迅速增长，通过无人机可打造短途航空物流网络，加速物流效率．某公司采用“站点对站点”的无人机快递运送模式，选用了A，B两种型号的无人机，已知A型号无人机平均每分钟比B型号无人机多飞行150米．若两站点之间的距离为5000米，A型号无人机单程所需时间是B型号无人机单程所需时间的 $\frac{4}{5}$ ，若不计停留时间，求A型号无人机在两站点之间往返的飞行时间．

查看试题解析
22. 综合与实践：图形的旋转变换是研究数学相关问题的重要手段之一，在研究三角形的旋转过程中，发现下列问题：如图1，在△ABC中， $A B = A C$ ， $∠ B A C = α$ ， D，E分别为AB，AC边上一点，连接DE，且 $D E ∥ B C$ ，将△ABC绕点A在平面内旋转．

(1)、观察猜想：若 $α = 60 °$ ，将△ABC绕点A旋转到如图2所示的位置，则DB与EC的数量关系为；

(2)、类比探究：若 $α = 90 °$ ，将△ABC绕点A旋转到如图3所示的位置，DB，CE相交于点O，猜想DB，CE满足的位置关系，并说明理由；

(3)、拓展应用：如图4，在（2）的条件下，连接CD，分别取DE，DC，BC的中点M，P，N，连接PM，PN，MN，若 $A D = 4$ ， $A B = 10$ ，请直接写出在旋转过程中△PMN面积的最大值．

查看试题解析
23. 综合与探究：如图，在平面直角坐标系 $x O y$ 中，四边形 $O A B C$ 是平行四边形， $A$ ， $C$ 两点的坐标分别为 $(4 ， 0)$ ， $(- 2 ， 3)$ ．将 $▱ O A B C$ 先向右平移4个单位后，再向下平移 $\frac{3}{2}$ 个单位，得到 $▱ O^{'} A^{'} B^{'} C^{'}$ ．

(1)、请你直接写出点 $O^{'}$ ， $C^{'}$ 的坐标；

(2)、平行四边形 $O^{'} A^{'} B^{'} C^{'}$ 与 $▱ O A B C$ 的重叠部分的形状是，重叠部分的面积是；

(3)、在平面内是否存在一点 $D$ ，使得以 $O$ ， $O^{'}$ ， $C^{'}$ ， $D$ 为顶点的四边形为平行四边形？若存在，请求出点 $D$ 的坐标；若不存在，请说明理由．

查看试题解析