山东省青岛市西海岸新区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
2. 如图,天平左盘中物体的质量为 , 天平右盘中每个砝码的质量都是 , 则的范围在数轴上可表示为( )
斐波那契螺旋线
2. 如图,天平左盘中物体的质量为 , 天平右盘中每个砝码的质量都是 , 则的范围在数轴上可表示为( )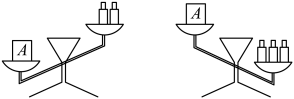 A、
A、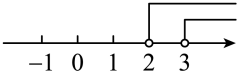 B、
B、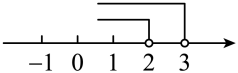 C、
C、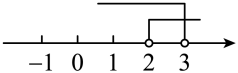 D、
D、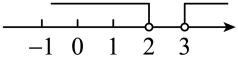 3. 若把分式的和同时扩大为原来的5倍,则分式的值( )A、扩大为原来的5倍 B、缩小为原来的 C、扩大为原来的10倍 D、保持不变4. 下列多项式中不能运用公式法进行因式分解的是( )A、 B、 C、 D、5. 正八边形和下列哪种正多边形可以镶嵌整个平面( )A、
3. 若把分式的和同时扩大为原来的5倍,则分式的值( )A、扩大为原来的5倍 B、缩小为原来的 C、扩大为原来的10倍 D、保持不变4. 下列多项式中不能运用公式法进行因式分解的是( )A、 B、 C、 D、5. 正八边形和下列哪种正多边形可以镶嵌整个平面( )A、 B、
B、 C、
C、 D、
D、 6. 若平行四边形的一条边长为9,则它的两条对角线长可能是( )A、3和4 B、5和6 C、6和8 D、10和127. 如图,的顶点坐标 , , , 将先向左平移3个单位,再向下平移1个单位,得到 , 则边上一点的对应点的坐标是( )
6. 若平行四边形的一条边长为9,则它的两条对角线长可能是( )A、3和4 B、5和6 C、6和8 D、10和127. 如图,的顶点坐标 , , , 将先向左平移3个单位,再向下平移1个单位,得到 , 则边上一点的对应点的坐标是( )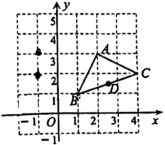 A、 B、 C、 D、8. 如图,是一钢架, , 为使钢架更加牢固,需在其内部添加一些钢管 , , , …,添加的钢管长度都与的长度相等,则最多能添加的钢管根数为( )
A、 B、 C、 D、8. 如图,是一钢架, , 为使钢架更加牢固,需在其内部添加一些钢管 , , , …,添加的钢管长度都与的长度相等,则最多能添加的钢管根数为( ) A、4 B、5 C、6 D、无数
A、4 B、5 C、6 D、无数二、填空题
-
9. 若一个分式只含有字母且当时分式的值为0,这个分式可以是(写出满足条件的一个分式即可)10. 已知,在数轴上表示实数的点与原点的距离不大于6,则的取值范围是 .11. 如图,平行四边形的周长是 , , 相交于点 , 交于点 , 则的周长是 .
 12. 已知 , , 则 .13. 若关于的分式方程有增根,则的值为 .14. 如图,直线与轴交于点 , 与直线相交于点 . 则关于的不等式组的解集是 .
12. 已知 , , 则 .13. 若关于的分式方程有增根,则的值为 .14. 如图,直线与轴交于点 , 与直线相交于点 . 则关于的不等式组的解集是 .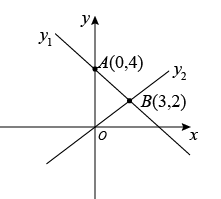 15. 如图,在中, , , 点 , 分别在 , 边上,将沿折叠,点恰好落在边的点上.若平分 , , 则 .
15. 如图,在中, , , 点 , 分别在 , 边上,将沿折叠,点恰好落在边的点上.若平分 , , 则 .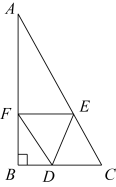 16. 如图,在平面直角坐标系中,点 , 的坐标分别为 , , 将绕原点顺时针旋转60°再将其各边都扩大为原来的2倍,使得 , , 得到 . 将绕原点顺时针旋转60°再将其各边都扩大为原来的2倍,使得 , , 得到 , …,如此继续下去,得到 , 则点的坐标是 .
16. 如图,在平面直角坐标系中,点 , 的坐标分别为 , , 将绕原点顺时针旋转60°再将其各边都扩大为原来的2倍,使得 , , 得到 . 将绕原点顺时针旋转60°再将其各边都扩大为原来的2倍,使得 , , 得到 , …,如此继续下去,得到 , 则点的坐标是 .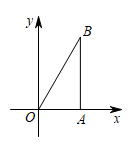
三、解答题
-
17.(1)、因式分解:;(2)、化简:;(3)、解不等式组:;(4)、解方程: .18. 已知:如图,及射线上的一点 .
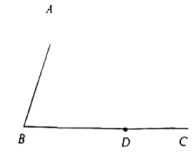 (1)、求作:等腰 , 使线段为等腰的底边,点在内部,且点到两边的距离相等(尺规作图,保留作图痕迹);(2)、在(1)的条件下,若 , 则 .19. 如图,在中,点是边的中点,平分角 , 连接交于点 , , 连接 . 已知 , , .
(1)、求作:等腰 , 使线段为等腰的底边,点在内部,且点到两边的距离相等(尺规作图,保留作图痕迹);(2)、在(1)的条件下,若 , 则 .19. 如图,在中,点是边的中点,平分角 , 连接交于点 , , 连接 . 已知 , , .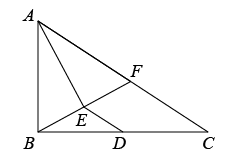 (1)、求证:;(2)、求的周长.20. 某校为开展“七彩六月,让梦齐飞”系列主题竞赛活动,学校决定到文体超市购买钢笔和笔记本共50件作为奖品,但购买奖品的总费用不能超过500元.已知钢笔的标价为15元/支,笔记本的标价为10元/本.经协商,超市老板同意钢笔、笔记本均按标价的8折给予优惠,那么学校最多能购买多少支钢笔?21. 如图,在与中, , , 点是边上的一点,且 . 连接 , 过点交作交的延长线于点 , 连接 .
(1)、求证:;(2)、求的周长.20. 某校为开展“七彩六月,让梦齐飞”系列主题竞赛活动,学校决定到文体超市购买钢笔和笔记本共50件作为奖品,但购买奖品的总费用不能超过500元.已知钢笔的标价为15元/支,笔记本的标价为10元/本.经协商,超市老板同意钢笔、笔记本均按标价的8折给予优惠,那么学校最多能购买多少支钢笔?21. 如图,在与中, , , 点是边上的一点,且 . 连接 , 过点交作交的延长线于点 , 连接 . (1)、证明:;(2)、判断四边形的形状,并证明你的结论.22. 中国是最早发现和利用茶树的国家,被称为茶的祖国.某茶店用8000元购进A种茶叶若干盒,用7800元购进种茶叶若干盒,所购A种茶叶比种茶叶多10盒,已知种茶叶的每盒进价是A种茶叶每盒进价的1.3倍.(1)、 , 两种茶叶的每盒进价分别为多少元?(2)、当购进的所有茶叶全部售完后,茶店以相同的进价再次购进 , 两种茶叶共150盘,且A种茶叶的数量不少于种茶叶的2倍.若A种茶叶的售价是每盒300元,种茶叶的售价为每盒400元,则A,两种茶叶分别购进多少盒时可使获得的利润最大?最大利润是多少?23. [阅读材料]:把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、解方程、求最值问题等中都有着广泛的应用.
(1)、证明:;(2)、判断四边形的形状,并证明你的结论.22. 中国是最早发现和利用茶树的国家,被称为茶的祖国.某茶店用8000元购进A种茶叶若干盒,用7800元购进种茶叶若干盒,所购A种茶叶比种茶叶多10盒,已知种茶叶的每盒进价是A种茶叶每盒进价的1.3倍.(1)、 , 两种茶叶的每盒进价分别为多少元?(2)、当购进的所有茶叶全部售完后,茶店以相同的进价再次购进 , 两种茶叶共150盘,且A种茶叶的数量不少于种茶叶的2倍.若A种茶叶的售价是每盒300元,种茶叶的售价为每盒400元,则A,两种茶叶分别购进多少盒时可使获得的利润最大?最大利润是多少?23. [阅读材料]:把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、解方程、求最值问题等中都有着广泛的应用.例1:用配方法因式分解: .
原式
例2:求的最小值.
解:;
由于 , 所以 ,
即的最小值为5.
(1)、[类比应用]:在横线上添上一个常数项使之成为完全平方式:;(2)、仿照例1的步骤,用配方法因式分解:;(3)、仿照例2的步骤,求的最小值;(4)、若 , 则 .24. 如图,在四边形中, , , , , 点从点出发,沿方向匀速运动,速度为;同时,点从点出发,沿方向匀速运动,速度为 . 过点作 , 垂足为 , 与相交于点 , 连接 . 设运动时间为 , 解答下列问题:
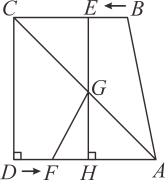 (1)、求的长度(用含的代数式表示);(2)、当时,求的值;(3)、设四边形的面积为 , 求与之间的关系式;(4)、在运动过程中,是否存在某一时刻,使得以点 , , , 为顶点的四边形为平行四边形?若存在,请直接写出的值;若不存在,请说明理由.
(1)、求的长度(用含的代数式表示);(2)、当时,求的值;(3)、设四边形的面积为 , 求与之间的关系式;(4)、在运动过程中,是否存在某一时刻,使得以点 , , , 为顶点的四边形为平行四边形?若存在,请直接写出的值;若不存在,请说明理由.