山东省聊城市高唐县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、3.1415 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 不等式的解集是( )A、 B、 C、 D、4. 如图所示,D,E,F分别是△ABC三边的中点,添加下列条件后,不能得到四边形DBFE是菱形的是( )
 A、AB=BC B、BE平分∠ABC C、BE⊥AC D、AB=AC5. 如图,中, , 则的值为( )
A、AB=BC B、BE平分∠ABC C、BE⊥AC D、AB=AC5. 如图,中, , 则的值为( ) A、6 B、 C、7 D、86. 如图,直线y=kx+b(k≠0)与x轴交于点(﹣5,0),下列说法正确的是( )
A、6 B、 C、7 D、86. 如图,直线y=kx+b(k≠0)与x轴交于点(﹣5,0),下列说法正确的是( )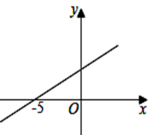 A、k>0,b<0 B、直线上两点(x1 , y1),(x2 , y2),若 , 则 C、直线经过第四象限 D、关于x的方程kx+b=0的解为x=﹣57. 如果不等式组的解集是 , 那么m的取值范围是( )A、 B、 C、 D、8. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )
A、k>0,b<0 B、直线上两点(x1 , y1),(x2 , y2),若 , 则 C、直线经过第四象限 D、关于x的方程kx+b=0的解为x=﹣57. 如果不等式组的解集是 , 那么m的取值范围是( )A、 B、 C、 D、8. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )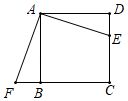 A、4 B、 C、6 D、9. 如图,在菱形中,P为对角线上一点.若 , 则的长为( )
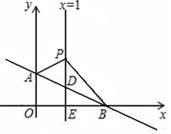
A、4 B、 C、6 D、9. 如图,在菱形中,P为对角线上一点.若 , 则的长为( )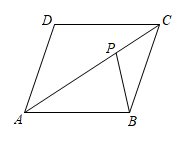 A、 B、 C、 D、10. 若一次函数 ( 为常数,且 )的图象经过点 , ,则不等式 的解为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,的顶点都在方格纸的格点上,将绕着某点顺时针旋转一定的角度后,得到 , 则旋转中心的坐标为( )
A、 B、 C、 D、10. 若一次函数 ( 为常数,且 )的图象经过点 , ,则不等式 的解为( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,的顶点都在方格纸的格点上,将绕着某点顺时针旋转一定的角度后,得到 , 则旋转中心的坐标为( )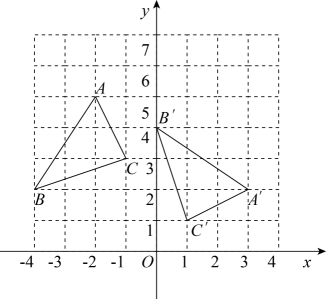 A、(-1,1) B、(-1,2) C、(1,1) D、(1,-1)12. 如图①,在边长为4cm正方形 ABCD 中,点P从点A出发,沿AB→BC的路径匀速运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时图象如图②所示.当P运动2.5s时,PQ的长为( )
A、(-1,1) B、(-1,2) C、(1,1) D、(1,-1)12. 如图①,在边长为4cm正方形 ABCD 中,点P从点A出发,沿AB→BC的路径匀速运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时图象如图②所示.当P运动2.5s时,PQ的长为( )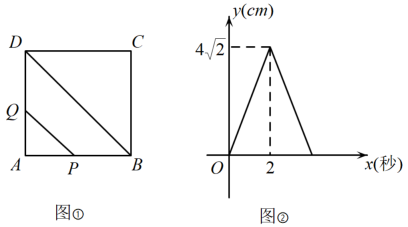 A、cm B、cm C、cm D、cm
A、cm B、cm C、cm D、cm二、填空题
-
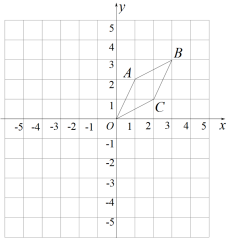
13. 函数中,自变量的取值范围是 .14. 计算÷3×的结果是 .15. 如图,在直角坐标系中,已知菱形的顶点 . 作菱形关于y轴的对称图形 , 再作图形关于点O的中心对称图形 , 则点C的对应点的坐标是 .
 16. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC,交BD于点O,则BD的长为 .
16. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC,交BD于点O,则BD的长为 .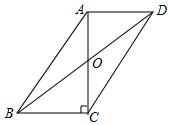 17. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.
17. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.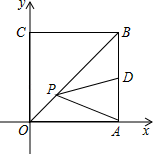
三、解答题
-
18. 计算:(1)、;(2)、 .19. 解不等式(组):(1)、解不等式: , 并求出非负整数解.(2)、解不等式组 , 并把解集表示在数轴上.
 20. 如图,在直角坐标系中,已知点和 , 请按下列要求画图并填空.
20. 如图,在直角坐标系中,已知点和 , 请按下列要求画图并填空.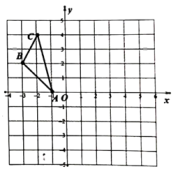 (1)、作出关于原点O成中心对称的 , 并直接写出点C的对应点的坐标 ▲ ;(2)、平移 , 使点平移到点处,作出平移后的 , 并直接写出点的对应点的坐标 ▲ ;(3)、直接写出四边形的面积 .21. 如图,是的垂直平分线,交于点M,过点M作 , 垂足分别为点E,F,已知 . 求证:四边形是正方形.
(1)、作出关于原点O成中心对称的 , 并直接写出点C的对应点的坐标 ▲ ;(2)、平移 , 使点平移到点处,作出平移后的 , 并直接写出点的对应点的坐标 ▲ ;(3)、直接写出四边形的面积 .21. 如图,是的垂直平分线,交于点M,过点M作 , 垂足分别为点E,F,已知 . 求证:四边形是正方形.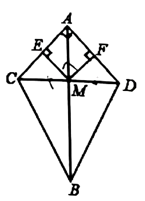 22. 如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
22. 如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.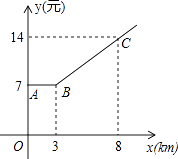 (1)、根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(1)、根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)、某人乘坐13km,应付多少钱?(3)、若某人付车费42元,出租车行驶了多少千米?23. 冰墩墩(BingDwenDwen),是2022年北京冬季奥运会的吉祥物.将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员.冬奥会来临之际,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶
B款玩偶
进货价(元/个)
20
15
销售价(元/个)
28
20
(1)、第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)、第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?