山东省济宁市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列根式是最简二次根式的是( )A、 B、 C、 D、2. 已知= , 则的值为( )A、 B、 C、 D、3. 下列计算,正确的是 ( )A、 B、 C、 D、4. 如图,有三个矩形,其中是相似图形的是( )
 A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙5. 解一元二次方程x2+4x-1=0,配方正确的是( )A、 B、 C、 D、6. 如图, , 下面等式成立的是( )
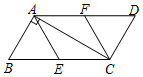
A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙5. 解一元二次方程x2+4x-1=0,配方正确的是( )A、 B、 C、 D、6. 如图, , 下面等式成立的是( )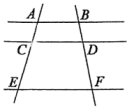 A、 B、 C、 D、7. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加株花苗,下面列出的方程中正确的是( )A、 B、 C、 D、8. 在中,点D是边上的点(与B,C两点不重合),过点D作 , 分别交 , 于E,F两点,下列说法正确的是( )
A、 B、 C、 D、7. 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为20元,需要每盆增加几株花苗?设每盆增加株花苗,下面列出的方程中正确的是( )A、 B、 C、 D、8. 在中,点D是边上的点(与B,C两点不重合),过点D作 , 分别交 , 于E,F两点,下列说法正确的是( )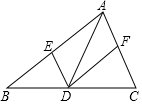 A、若 , 则四边形是矩形 B、若垂直平分 , 则四边形是矩形 C、若 , 则四边形是菱形 D、若平分 , 则四边形是菱形9. 若关于x的一元二次方程()有一根为 , 则一元二次方程必有一根为( )A、2020 B、2021 C、2022 D、202310. 如图,在菱形中, , 交BC的延长线于点E.连接AE交BD于点F,交CD于点G、于点H,连接CF.有下列结论:①;②;③;④ . 其中正确结论个数为( )
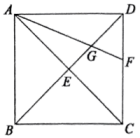
A、若 , 则四边形是矩形 B、若垂直平分 , 则四边形是矩形 C、若 , 则四边形是菱形 D、若平分 , 则四边形是菱形9. 若关于x的一元二次方程()有一根为 , 则一元二次方程必有一根为( )A、2020 B、2021 C、2022 D、202310. 如图,在菱形中, , 交BC的延长线于点E.连接AE交BD于点F,交CD于点G、于点H,连接CF.有下列结论:①;②;③;④ . 其中正确结论个数为( )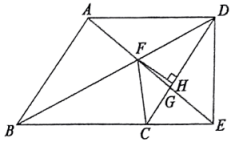 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 如图,在直角坐标系中,与是位似图形,则位似中心的坐标为 .
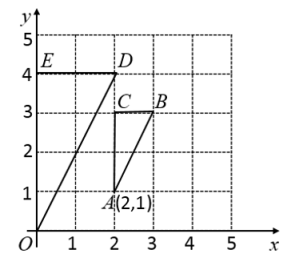 13. 某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .14. 如图,将正方形纸片折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
13. 某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为 .14. 如图,将正方形纸片折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .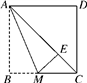 15. 对于实数 , ,定义一种运算 为: 如果关于 的方程 有两个相等的实数根,则 .
15. 对于实数 , ,定义一种运算 为: 如果关于 的方程 有两个相等的实数根,则 .三、解答题
-
16. 计算:(1)、(2)、17. 解方程:(1)、(2)、18. 如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.
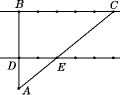 19. 某市某水果批发市场某批发商原计划以每千克10元的单价对外批发销售某种水果.为了加快销售,该批发商对价格进行两次下调后,售价降为每千克6.4元.(1)、求平均每次下调的百分率;(2)、某大型超市准备到该批发商处购买2吨该水果,因数量较多,该批发商决定再给予两种优惠方案以供选择.方案一:打八折销售;方案二:不打折,每吨优惠现金1000元.试问超市采购员选择哪种方案更优惠?请说明理由.20. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
19. 某市某水果批发市场某批发商原计划以每千克10元的单价对外批发销售某种水果.为了加快销售,该批发商对价格进行两次下调后,售价降为每千克6.4元.(1)、求平均每次下调的百分率;(2)、某大型超市准备到该批发商处购买2吨该水果,因数量较多,该批发商决定再给予两种优惠方案以供选择.方案一:打八折销售;方案二:不打折,每吨优惠现金1000元.试问超市采购员选择哪种方案更优惠?请说明理由.20. 在▱ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.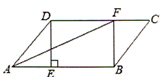 (1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.21. 某市进行“三改一拆”治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长是8m的正方形ABCD,改建的绿地是矩形AEFG,其中点E在AB上点,G在AD的延长线上,且DG=2BE,如果设BE的长为x(单位:m).
(1)、求证:四边形BFDE是矩形;(2)、若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.21. 某市进行“三改一拆”治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长是8m的正方形ABCD,改建的绿地是矩形AEFG,其中点E在AB上点,G在AD的延长线上,且DG=2BE,如果设BE的长为x(单位:m).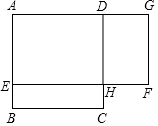 (1)、用含有x的代数式表示绿地AEFG的面积;(2)、当x取何值时,绿地AEFG的面积为70m2?
(1)、用含有x的代数式表示绿地AEFG的面积;(2)、当x取何值时,绿地AEFG的面积为70m2?