河北省张家口市宣化区2021-2022学年八年级下学期期末考试数学(人教版)试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 =±6 B、4 ﹣3 =1 C、 =6 D、 =62. 为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:
每天锻炼时间(分钟)
20
40
60
90
学生数
2
3
4
1
则关于这些同学的每天锻炼时间,下列说法错误的是( )
A、众数是60 B、平均数是21 C、抽查了10个同学 D、中位数是503. 若 =﹣a ,则a的取值范围是( )A、﹣3≤a≤0 B、a≤0 C、a<0 D、a≥﹣34. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、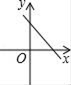 B、
B、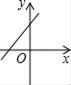 C、
C、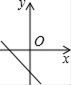 D、
D、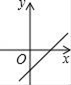 5. 将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为( ).
5. 将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为( ). A、3 B、3 C、2 D、6. 对于一次函数 , 下列叙述正确的是( )A、当时,函数图象经过第一、二、三象限 B、当时,y随x的增大而增大 C、当时,函数图象一定不经过第二象限 D、函数图象一定经过点7. 根据如图所示的程序计算函数y的值,若输入x的值是8,则输出y的值是 , 若输入x的值是 , 则输出y的值是( )
A、3 B、3 C、2 D、6. 对于一次函数 , 下列叙述正确的是( )A、当时,函数图象经过第一、二、三象限 B、当时,y随x的增大而增大 C、当时,函数图象一定不经过第二象限 D、函数图象一定经过点7. 根据如图所示的程序计算函数y的值,若输入x的值是8,则输出y的值是 , 若输入x的值是 , 则输出y的值是( ) A、10 B、14 C、18 D、228. 如图,正方形ABCD的边长为 ,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( )
A、10 B、14 C、18 D、228. 如图,正方形ABCD的边长为 ,对角线AC,BD交于点O,E是AC延长线上一点,且CE=CO.则BE的长度为( ) A、 B、 C、 D、9. 直线y=﹣x+1与y=2x+a的交点在第一象限,则a的取值不可能是( )A、 B、﹣ C、﹣ D、﹣10. 如图,E、F分别是▱ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若 , ,则阴影部分的面积为( )
A、 B、 C、 D、9. 直线y=﹣x+1与y=2x+a的交点在第一象限,则a的取值不可能是( )A、 B、﹣ C、﹣ D、﹣10. 如图,E、F分别是▱ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若 , ,则阴影部分的面积为( ) A、40 B、45 C、50 D、5511. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
A、40 B、45 C、50 D、5511. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ). A、80 B、88 C、96 D、10012. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论中错误的是( )
A、80 B、88 C、96 D、10012. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论中错误的是( ) A、乙的速度为5米/秒 B、乙出发8秒钟将甲追上 C、当乙到终点时,甲距离终点还有96米 D、a对应的值为123
A、乙的速度为5米/秒 B、乙出发8秒钟将甲追上 C、当乙到终点时,甲距离终点还有96米 D、a对应的值为123二、填空题
-
13. 函数y= 中自变量x的取值范围是14. 直线y=﹣2x+b过点(3,1),将它向下平移4个单位后所得直线的解析式是 .15. 评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试85分,作业90分,课堂参与80分,则他的数学期末成绩为分.16. 如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面的部分 为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部 恰好碰到岸边的 ,则这根芦苇的长度是尺.
 17. 在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A,C分别在x轴和y轴上,OA=4,OC=3,D为AB边的中点,E是OA边上的一个动点,当△CDE的周长最小时,则点E的坐标为 .
17. 在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A,C分别在x轴和y轴上,OA=4,OC=3,D为AB边的中点,E是OA边上的一个动点,当△CDE的周长最小时,则点E的坐标为 . 18. 如图,矩形 中, ,点E是 边上一点,连接 ,把 沿 折叠,使点B落在点F处,当 为直角三角形时, 的长为.
18. 如图,矩形 中, ,点E是 边上一点,连接 ,把 沿 折叠,使点B落在点F处,当 为直角三角形时, 的长为.
三、解答题
-
19. 计算:20. 某校利用自身的体育特色,因地制宜开展垫球运动,如图图表中的数据分别是甲、乙、丙3名学生10次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
运动员甲测试成绩统计表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
 (1)、学生甲测试成绩的众数是 , 中位数是 .(2)、已知(分), , 若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,分别求出 , , 并从平均数和方差两个角度综合分析选谁更合适.21. 已知点A(6,0)及在第一象限的动点P(x,10﹣x),设△OPA的面积为S.(1)、求S关于x的函数解析式,并求出x的取值范围;(2)、画出函数S的图象.22. 在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
(1)、学生甲测试成绩的众数是 , 中位数是 .(2)、已知(分), , 若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,分别求出 , , 并从平均数和方差两个角度综合分析选谁更合适.21. 已知点A(6,0)及在第一象限的动点P(x,10﹣x),设△OPA的面积为S.(1)、求S关于x的函数解析式,并求出x的取值范围;(2)、画出函数S的图象.22. 在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.已知:在△ABC中,D、E分别是边AB、AC的中点.
求证:.
证明:如图,延长DE到点F,使EF=DE,连接CF,
 (1)、补全求证;(2)、请根据添加的辅助线,写出完整的证明过程.23. 疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩 袋,该企业购买口罩的总费用为 元.(1)、请求出 与 的函数关系式;(2)、已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
(1)、补全求证;(2)、请根据添加的辅助线,写出完整的证明过程.23. 疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩 袋,该企业购买口罩的总费用为 元.(1)、请求出 与 的函数关系式;(2)、已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.

