河北省石家庄市辛集市2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 式子有意义的x的取值范围是( )A、 B、 C、 D、且2. 如图,在的正方形网格中,若小正方形的边长是1,则任意两个格点间的距离不可能是( )
 A、 B、 C、3 D、3. 下列说法正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直且平分的四边形是正方形 D、对角线互相垂直的四边形是菱形4. 将直线向下平移6个单位长度后得到直线 , 则下列关于直线说法正确的是( )A、图象经过一、二、四象限 B、当时, C、图象与x轴交于 D、直线与坐标轴围成的三角形的面积为25. 下列根式:① ;② ;③ ;④ ,化为最简二次根式后,被开方数相同的是( )A、①和② B、②和③ C、③和④ D、①和④6. 一个直角三角形的两边长分别为8cm、10cm,则第三条边长为( )A、6cm B、12cm C、cm D、6cm 或cm7. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是2,则AB的长为( )
A、 B、 C、3 D、3. 下列说法正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直且平分的四边形是正方形 D、对角线互相垂直的四边形是菱形4. 将直线向下平移6个单位长度后得到直线 , 则下列关于直线说法正确的是( )A、图象经过一、二、四象限 B、当时, C、图象与x轴交于 D、直线与坐标轴围成的三角形的面积为25. 下列根式:① ;② ;③ ;④ ,化为最简二次根式后,被开方数相同的是( )A、①和② B、②和③ C、③和④ D、①和④6. 一个直角三角形的两边长分别为8cm、10cm,则第三条边长为( )A、6cm B、12cm C、cm D、6cm 或cm7. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是2,则AB的长为( ) A、1 B、 C、2 D、8. 某轮滑队所有队员的年龄只有12、13、14、15、16(岁)五种情况,其中部分数据如图所示,若队员年龄的唯一的众数与中位数相等,则这个轮滑队队员人数m最小是( )
A、1 B、 C、2 D、8. 某轮滑队所有队员的年龄只有12、13、14、15、16(岁)五种情况,其中部分数据如图所示,若队员年龄的唯一的众数与中位数相等,则这个轮滑队队员人数m最小是( )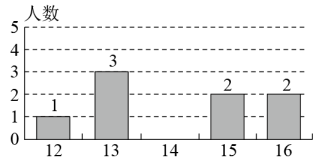 A、9 B、10 C、11 D、129. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、
A、9 B、10 C、11 D、129. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、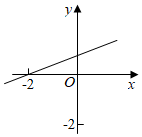 B、
B、 C、
C、 D、
D、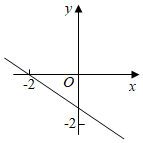 10. 在中,D,E分别是边AB,AC的中点,按图中方法作图后,若四边形ABHG的周长与的周长相等,还需具备的条件是( )
10. 在中,D,E分别是边AB,AC的中点,按图中方法作图后,若四边形ABHG的周长与的周长相等,还需具备的条件是( ) A、 B、 C、 D、11. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=135,S3=49,则S2=( )
A、 B、 C、 D、11. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=135,S3=49,则S2=( ) A、184 B、86 C、119 D、8112. 某组数据方差计算公式为: , 由公式提供的信息,下列说法错误的是( )A、样本的容量是3 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是313. 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点 P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为 ( )
A、184 B、86 C、119 D、8112. 某组数据方差计算公式为: , 由公式提供的信息,下列说法错误的是( )A、样本的容量是3 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是313. 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点 P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为 ( ) A、10 B、5 C、10-10 D、10-514. 如图,在平面直角坐标系中,等边的顶点在原点上,在轴上, , 为边的中点,将等边向右平移,当点落在直线:上时,点的对应点的坐标为( )
A、10 B、5 C、10-10 D、10-514. 如图,在平面直角坐标系中,等边的顶点在原点上,在轴上, , 为边的中点,将等边向右平移,当点落在直线:上时,点的对应点的坐标为( )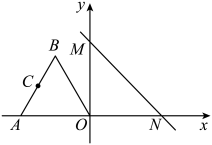 A、 B、 C、 D、15. 已知T1= ,T2= ,T3= , ,Tn= ,其中 为正整数.设Sn=T1+T2+T3+ +Tn , 则S2021值是( )A、 B、 C、 D、16. 跳远运动员李强在一次训练中,先跳了6次的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m).这六次成绩的平均数为7.8,方差为 . 如果李强再跳两次,成绩分别为7.6,8.0,则李强这8次跳远成绩与前6次的成绩相比较,其方差 ( ).A、变大 B、变小 C、不变 D、无法确定
A、 B、 C、 D、15. 已知T1= ,T2= ,T3= , ,Tn= ,其中 为正整数.设Sn=T1+T2+T3+ +Tn , 则S2021值是( )A、 B、 C、 D、16. 跳远运动员李强在一次训练中,先跳了6次的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m).这六次成绩的平均数为7.8,方差为 . 如果李强再跳两次,成绩分别为7.6,8.0,则李强这8次跳远成绩与前6次的成绩相比较,其方差 ( ).A、变大 B、变小 C、不变 D、无法确定二、填空题
-
17. 已知 ,化简: .18. 在四边形ABCD中,ADBC,BC⊥CD,AD=6cm,BC=10cm,M是BC上一点,且BM=4,点E从A出发以1cm/s的速度向D运动,点F从点B出发以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,当t的值为 时,以A、M、E、F为顶点的四边形是平行四边形.
 19. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 .
19. 如图,平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD,点C的坐标是 . 在y轴上有一个动点M,当△MDC的周长最小的时候,点M的坐标是 .
三、解答题
-
20. 计算:(1)、;(2)、 .21. 如图,AD是△ABC的中线,DE⊥AC于点E,DF是△ABD的中线,且CE=2,DE=4,AE=8.
 (1)、求证:;(2)、求DF的长.22. 如图,在中,AC=BC,M、N分别是AB和CD的中点.
(1)、求证:;(2)、求DF的长.22. 如图,在中,AC=BC,M、N分别是AB和CD的中点. (1)、求证:四边形AMCN是矩形;(2)、若∠B=60°,BC=8,求的面积.23. 某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列,)三位入围者的成绩(百分制,成绩都是整数)如下表:
(1)、求证:四边形AMCN是矩形;(2)、若∠B=60°,BC=8,求的面积.23. 某公司欲招聘一名销售人员,按1:3的比例入围的甲、乙、丙(笔试成绩没有相同的,按从高到低排列,)三位入围者的成绩(百分制,成绩都是整数)如下表:入围者
笔试成绩
面试成绩
甲
90
86
乙
x
x
丙
84
92
(1)、若公司认为笔试成绩与面试成绩同等重要,结果乙被录取,求x的值;(2)、若公司认为笔试成绩与面试成绩按4:6的权重,结果乙排第二,丙被录取,求x的值;(3)、若公司认为笔试成绩与面试成绩按a:(10-a)(a为1~9的整数)的权重,为确保甲被录取,求a的最小值.24. 甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地.甲车出发40min后乙车出发,乙车匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50km/h,结果乙车与甲车同时到达B地,甲、乙两车离A地的距离y(km)与乙车行驶时间x(h)之间的函数图象如图所示.
请根据相关信息,解答下列问题:
(1)、图中a=;(2)、①A、B两地的距离为km;甲车行驶全程所用的时间为h;甲的速度是km/h;点C的坐标为;②直接写出线段CF对应的函数表达式;
③当乙刚到达货站时,甲距离B地还有km.
(3)、乙车出发小时在途中追上甲车;(4)、乙出发小时,甲乙两车相距50km.25. 某草莓种植基地专门种植草莓并批发出售给超市,草莓的批发总金额y(元)与批发量x(斤)是正比例函数关系,比例系数为k,当x=10时,y=250.(1)、求y与x的函数关系式为 , k 的实际意义为;(2)、近日,该基地让利超市:超市一次性批发购进草莓100斤及以下,不优惠;一次性批发购进草莓100斤以上,超过100斤的部分单价打8折.若某超市每天都从该基地批发购进草莓x (斤) (x≥90)并以35元斤的价格全部售出,设超市每天销售草莓获得的利润为w元(不考虑销售过程中的损耗).①求w与x的函数关系式,并写出x的取值范围;
②某一天该超市销售草莓的利润为1900元,求购进草莓的数量.
26. 直线与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E. (1)、请直接写出点C,点D的坐标,并求出m的值;(2)、点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M,交CE于N.当四边形NEDM是平行四边形时,求点P的坐标;(3)、点P(0,t)是y轴正半轴上的一个动点,Q是平面内任意一点,t为何值时,以点C、D、P、Q为顶点的四边形是菱形?
(1)、请直接写出点C,点D的坐标,并求出m的值;(2)、点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M,交CE于N.当四边形NEDM是平行四边形时,求点P的坐标;(3)、点P(0,t)是y轴正半轴上的一个动点,Q是平面内任意一点,t为何值时,以点C、D、P、Q为顶点的四边形是菱形?