北京市海淀区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{12}$ B、 $\sqrt{2}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{1.5}$

查看试题解析
2. 以下列长度的三条线段为边，能组成直角三角形的是（）

A、2，3，4 B、 $\sqrt{7}$ ， 3，5 C、6，8，10 D、5，12，12

查看试题解析
3. 某函数的图象如图所示，随着x的增大，函数y（）

A、增大 B、减小 C、不变 D、有时增大有时减小

查看试题解析
4. 如图，矩形ABCD的对角线AC，BD相交于点O， $∠ A O B = 60 °$ ， $A B = 4$ ，则矩形对角线的长为（）

A、4 B、8 C、 $4 \sqrt{3}$ D、 $4 \sqrt{5}$

查看试题解析
5. 如图，在 $▱ A B C D$ 中， $A D = 6$ ， E为AD上一动点，M，N分别为BE，CE的中点，则MN的长为（）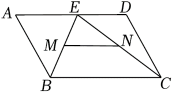

A、4 B、3 C、2 D、不确定

查看试题解析
6. 下表记录了四名同学最近几次一分钟踢毽子选拔赛成绩的平均数与方差．
姓名
甲
乙
丙
丁
平均数
74.25
70
70
65.75
方差
3.07
4.28
2.57
6.78
根据表中数据，要从中选择两名成绩更好且发挥稳定的同学参加正式比赛，应选择（）

A、甲和乙 B、乙和丙 C、甲和丁 D、甲和丙

查看试题解析
7. 如图，有一架秋千，当它静止时，踏板离地0.5米，将它往前推3米时，踏板离地1.5米，此时秋千的绳索是拉直的，则秋千的长度是（）

A、3米 B、4米 C、5米 D、6米

查看试题解析
8. 如图，分别在四边形ABCD的各边上取中点E，F，G，H，连接EG，在EG上取一点M，连接HM，过F作 $F N ∥ H M$ ，交EG于N，将四边形ABCD中的四边形①和②移动后按图中方式摆放，得到四边形 $A H M^{'} G^{'}$ 和 $A F^{'} N^{'} E$ ，延长 $M^{'} G^{'}$ ， $N^{'} F^{'}$ 相交于点K，得到四边形 $M M^{'} K N^{'}$ ．下列说法中，错误的是（）

A、 $S_{四边形 M M^{'} K N^{'}} = S_{四边形 A B C D}$ B、 $H M = N F$ C、四边形 $M M^{'} K N^{'}$ 是平行四边形 D、 $∠ K = ∠ A H M^{'}$

查看试题解析

二、填空题

9. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
10. 比较大小：2 $\sqrt{3}$ 4．（填“＞”、“＜”或“＝”号）

查看试题解析
11. 若一次函数的图象过点 $(0 ， 3)$ ，请写出一个符合条件的函数解析式．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 40 °$ ， D为线段AB的中点，则 $∠ B C D =$ ．

查看试题解析
13. 菱形ABCD的面积为24cm² ，对角线BD的长为6cm，则AC的长为cm．

查看试题解析
14. 如图，直线 $y_{1} = 2 x$ 与 $y_{2} = - x + a$ 交于点 $P (1 ， 2)$ ，则不等式 $2 x > - x + a$ 的解集为．

查看试题解析
15. 某班有10名同学利用假期参与了社区志愿服务活动，他们的社区服务时长如下表所示．
服务时长（小时）
15
16
20
人数（人）
2
5
3
这10名同学社区服务的平均时长是小时．

查看试题解析
16. 如图，在平面直角坐标系xOy中．四边形OABC为正方形，点A的坐标为 $(3 ， 0)$ ．若直线 $l_{1}$ ： $y = - x + b_{1}$ 和直线 $l_{2}$ ： $y = - x + b_{2} (b_{1} \neq b_{2})$ 被正方形OABC的边所截得的线段长度相等，写山一组满足条件的 $b_{1}$ 与 $b_{2}$ 的值．

查看试题解析

三、解答题

17. 计算： $\sqrt{12} - \sqrt{3} + 3 \sqrt{\frac{1}{3}}$ ．

查看试题解析
18. 已知 $x = \sqrt{2} - 1$ ，求代数式 $x^{2} + 2 x - 3$ 的值．

查看试题解析
19. 已知：如图1， $△ A B C$ ，求作： $▱ A B C D$ ．
作法：①在AC边上任取点E，连接BE，以点C为圆心，AE长为半径画弧，交线段AC于点F；
②分别以点F，C为圆心，BE，AB长为半径画弧，两弧相交于点D，使点B和点D在AC的两旁；
③连接AD，DC．
四边形ABCD即为所求．

(1)、根据题意，在图2中补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接DF．
∵ $A E = C F$ ， $A B = C D$ ， $E B = F D$ ，
∴ $△ A B E ≌ △ C D F$ （SSS）．
∴  ▲   ．
∴ $A B ∥ C D$ （   ）（填推理的依据）．
∵ $A B = C D$ ，
∴四边形ABCD为平行四边形（    ）（填推理的依据）．

查看试题解析
20. 如图，在菱形ABCD中，E为AB边上一点，过点E作 $E F ∥ B C$ ，交BD于点M，交CD于点F．求证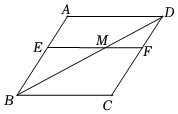： $C F = E M$ ．

查看试题解析
21. 如图，在正方形网格中，每个小正方形的边长都是1，点A，B，C，D是网格线的交点．

(1)、求证： $∠ A D C = 90 °$ ；

(2)、四边形ABCD的面积为．

查看试题解析
22. 在平面直角坐标系xOy中，直线 $y = \frac{1}{2} x + 2$ 与x轴相交于点A，与y轴相交于点B．

(1)、求点A和点B的坐标；

(2)、点P为直线 $y = \frac{1}{2} x + 2$ 上一动点，若 $△ O B P$ 的面积为3，则点P的坐标为．

查看试题解析
23. 水龙头关闭不严会造成滴水．下表记录了30min内7个时间点的漏水量，其中t表示时间，y表示漏水量．
时间t/min
0
5
10
15
20
25
30
漏水量y/mL
0
15
30
45
60
75
90
解决下列问题：

(1)、在平面直角坐标系中，描出上表中以各对对应值为坐标的点，根据描出的点连线；

(2)、结合表中数据写出滴水量y关于时间t的函数解析式（不要求写自变量的取值范围）；

(3)、在这种漏水状态下，若不及时关闭水龙头，估算一天的漏水量约为mL．

查看试题解析
24. 如图，在 $△ A B C$ 中，D是AB上一点， $A D = D C$ ， DE平分∠ADC交AC于点E，DF平分∠BDC交BC于点F， $∠ D F C = 90 °$ ．

(1)、求证：四边形CEDF是矩形；

(2)、若 $∠ B = 30 °$ ， $A D = 2$ ，连接BE，求BE的长．

查看试题解析
25. 为比较营养液A和营养液B对某种小西红柿产量的影响，甲、乙两个生物小组各选取了10株长势相近的小西红柿秧苗进行对照实验，甲组使用营养液A，乙组使用营养液B．将每株的产量记录整理，并绘制了如下两个条形图．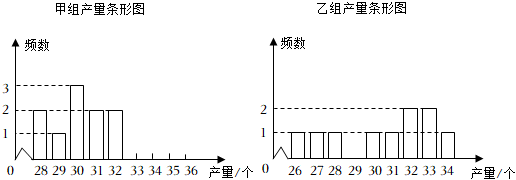
解答下列问题：

(1)、甲组产量的众数为，乙组产量的中位数为；

(2)、经过计算发现两组产量的平均数接近，为了使产量更稳定，则应选择营养液（填“A”或“B”）；

(3)、产量30个及以上为秧苗长势良好．现在选用第（2）问推荐的营养液培育100株秧苗，请估计长势良好的大约为株．

查看试题解析
26. 已知：在平面直角坐标系xOy中，直线 $l_{1}$ ： $y = k x + 3$ 与直线 $l_{2}$ ： $y = 2 x + 1$ ．

(1)、若直线 $l_{1}$ 与直线 $l_{2}$ 交于点 $A (2 ， m)$ ，求k，m的值；

(2)、过点 $B (n ， 0)$ 作垂直于x轴的直线分别交 $l_{1}$ ， $l_{2}$ 于点C，D，结合函数图象回答下列问题：
①当 $n = 1$ 时，若 $C D = 1$ ，求k的值；
②当 $- 1 < n < k + 2$ 时，在点B运动的过程中，CD恒大于1.请写出两个符合条件的k的值 ▲ ．

查看试题解析
27. 在等边 $△ A B C$ 中，D，E，F分别是边AB，BC，CA上的动点，满足 $D E = E F$ ，且 $∠ D E F = 60 °$ ．作点E关于AC的对称点G，连接CG，DG．

(1)、当点D，E，F在如图1所示的位置时，请在图1中补全图形，并证明四边形DBCG是平行四边形；

(2)、当 $A D < B D$ ， $A B = \sqrt{2} D E$ 时，求∠BDE的度数．

查看试题解析
28. 在平面直角坐标系xOy中，已知 $△ A B C$ 的顶点 $A (0 ， 1)$ ， $B (3 ， 2)$ ，对于点P和 $△ A B C$ ，给出如下定义：如果 $△ A B C$ 上存在三个点，使得以点P和这三个点为顶点的四边形是平行四边形，则称点P是 $△ A B C$ 的“平行连接点”．例如，图1中，C，P两点的坐标分别为 $(4 ， 1)$ ， $(5 ， 2)$ ， $△ A B C$ 上存在B，C和 $D (2 ， 1)$ 三个点，使得四边形PBDC是平行四边形，故点P是 $△ A B C$ 的“平行连接点”．

(1)、如图2，当点C的坐标为 $(3 ， 1)$ 时，
①点 $P_{1} (5 ， 2)$ ， $P_{2} (6 ， 2)$ ， $P_{3} (6 ， 3)$ ， $P_{4} (7 ， 2)$ 中，是 $△ A B C$ 的“平行连接点”的是 ▲ ；
②若 $P (m ， 0)$ 是 $△ A B C$ 的“平行连接点”，请在图2中画出一个以点P和 $△ A B C$ 上的三个点为顶点的平行四边形，这个平行四边形对角线交点的纵坐标为 ▲ ， m的取值范围为 ▲ ；

(2)、如图3，当点C的坐标为 $(1 ， 3)$ 时，直线 $y = k x - 2$ 上存在 $△ A B C$ 的“平行连接点”，则k的取值范围为．

查看试题解析

姓名	甲	乙	丙	丁
平均数	74.25	70	70	65.75
方差	3.07	4.28	2.57	6.78

服务时长（小时）	15	16	20
人数（人）	2	5	3

时间t/min	0	5	10	15	20	25	30
漏水量y/mL	0	15	30	45	60	75	90