北京市大兴区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）．

A、 $\sqrt{32}$ B、 $\sqrt{90}$ C、 $\sqrt{\frac{3}{2}}$ D、 $\sqrt{5}$

查看试题解析
2. 下列各组数中，能作为直角三角形的三边长的是（）．

A、1.5，2，3 B、2，3，4 C、1，1， $\sqrt{2}$ D、5，13，14

查看试题解析
3. 一个菱形的两条对角线的长分别是4和6，这个菱形的面积是（）．

A、6 B、10 C、12 D、24

查看试题解析
4. 下列图象中不能表示y是x的函数的是（）．

A、 B、 C、 D、

查看试题解析
5. 一次函数y＝x﹣1的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 某校学生参加区诗词大赛预选赛，经过多次测试后，有四位同学成为晋级的候选人，具体情况如下表，如果从这四位同学中选出一名总体水平高且成绩稳定的选手晋级，你会推荐（）．

甲
乙
丙
丁
平均分
94
94
92
92
方差
23
35
23
35

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图，菱形ABCD中， $∠ A = 30 °$ ， $A B = 4$ ，点E，F分别是边AB，CD的中点，动点P从点E出发，按逆时针方向，沿EB，BC，CF匀速运动到点F停止，设 $△ P A D$ 的面积为S，动点P运动的路径总长为x，能表示S与x函数关系的图象大致是（）．

A、 B、 C、 D、

查看试题解析
8. 如图，我们称四个顶点都恰好在格点的四边形为格点四边形，A，B为4×4的正方形网格中的两个格点，在此图中以A，B为顶点的格点四边形是平行四边形的个数是（）．

A、10 B、11 C、12 D、13

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 请写出一个y随x增大而增大的正比例函数表达式，y=

查看试题解析
11. 一次函数 $y = - 2 x + 3$ 的图象与y轴的交点坐标为．

查看试题解析
12. 如果将一次函数 $y = x + 8$ 的图象向下平移6个单位，那么所得图象的函数解析式是．

查看试题解析
13. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $(3 ， 2)$ ，且y随x的增大而减小，则不等式 $k x + b > 2$ 的解集为．

查看试题解析
14. 现有5名同学的身高分别为165，172，168，170，175（单位：厘米）．增加1名身高为170的同学后，这6名同学身高的平均数和方差与原来相比，平均数（填“变大”、“变小”“不变”），方差（填“变大”、“变小”、“不变”）．

查看试题解析
15. 如图，点E是正方形ABCD的对角线BD上一点， $E F ⊥ B C$ ， $E G ⊥ C D$ ，垂足分别是F，G， $G F = 5$ ，则AE＝．

查看试题解析
16. 已知直线 $y_{1} = a x + b (a \neq 0)$ 与直线 $y_{2} = k x + 5 (k \neq 0)$ 关于y轴对称，当 $x > - \frac{5}{2}$ 时， $y_{1} > 0$ ，当 $x > \frac{5}{2}$ 时， $y_{2} < 0$ ，则直线 $y_{1} =$ ．

查看试题解析

三、解答题

17. 计算： ${(π + \sqrt{2})}^{0} + \sqrt{45} - {(\frac{1}{2})}^{- 1} - | \sqrt{5} - 1 |$ ．

查看试题解析
18. 如图，在平面直角坐标系xOy中，直线 $l_{1} ： y_{1} = 2 x$ 与直线 $l_{2} ： y_{2} = - x + 3$ 交于点A．

(1)、求点A的坐标；

(2)、当 $y_{1} < y_{2}$ 时，直接写出x的取值范围．

查看试题解析
19. 在平面直角坐标系xOy中，一次函数的图象经过点 $A (- 2 ， 0)$ 与点 $B (0 ， 4)$ ．

(1)、求这个一次函数的解析式；

(2)、若点C是x轴上一点，且 $△ A B C$ 的面积是4，求点C的坐标．

查看试题解析
20. 如图，在 $▱ A B C D$ 中，对角线AC，BD交于点O，且点E，F分别是AO，CO的中点，连接BE，BF，DE，DF．求证：四边形BEDF是平行四边形．

查看试题解析
21. 下面是小明同学设计的“已知两条对角线长作菱形”的尺规作图过程．
已知：如图1，线段a．
求作：菱形ABCD，使得对角线 $A C = a$ ， $B D = 2 a$ ．
作法：如图2，
①作射线AM，并在射线AM上截取 $A C = a$ ；
②作线段AC的垂直平分线PQ，PQ交AC于点O；
③以点O为圆心，a为半径作弧，交PQ于点B，D；
④连接AB，AD，BC，CD．
则四边形ABCD为所求作的菱形．

(1)、用直尺和圆规，依作法补全图2中的图形（保留作图痕迹）；

(2)、完成下面的证明：
证明：由作图可知 $A C = a$ ， $B D = 2 a$ ．
∵PQ为线段AC的垂直平分线，∴ $O A = O C$ ．
∵ $O B = O D$ ，
∴四边形ABCD是平行四边形（）（填推理的依据）．
又∵ $A C ⊥ B D$ ， ∴ $▱ A B C D$ 是菱形（）（填推理的依据）．

查看试题解析
22. 某社区为了增强居民节约用水的意识，随机调查了部分家庭一年的月均用水量（单位：t）．
根据调查结果，绘制出如下的统计图①和图②．

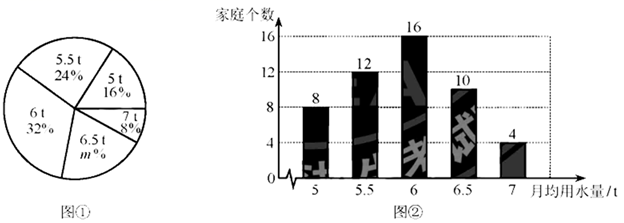
请根据相关信息，解答下列问题：

(1)、本次接受调查的家庭个数为，图①中m的值为；

(2)、求统计的这组月均用水量数据的平均数、众数和中位数．

查看试题解析
23. 已知直线y=x+5与x轴交于点A（x₁ ， 0），直线y=kx+1（k≠0）与x轴交于点B（x₂ ， 0），两直线交于点C（m，3）．

(1)、求m，k的值；

(2)、点P在直线 $y = x + 5$ 上，过点P作y轴的平行线，交直线 $y = k x + 1 (k \neq 0)$ 于点Q，若 $P Q = A B$ ，求点P的坐标．

查看试题解析
24. 已知学校、书店、图书馆依次在同一条直线上，书店离学校12km，图书馆离学校20km．李华从学校出发，匀速骑行0.6h到达书店；在书店停留0.4h后，匀速骑行0.5h到达图书馆；在图书馆参观学习一段时间，然后回学校；回学校途中，匀速骑行0.5h后减速，继续匀速骑行回到学校．给出的图象反映了这个过程中李华离学校的距离y（单位：km）与离开学校的时间x（单位：h）之间的对应关系．
请根据相关信息，解答下列问题：

(1)、填表：
离开学校的时间/h
0.1
0.5
0.8
1
3
离学校的距离/km
2
10
12

(2)、当 $0 \leq x \leq 1$ 时，请直接写出y关于x的函数解析式；

(3)、当李华离学校的距离为6km时，他离开学校的时间为h．

查看试题解析
25. 如图，在矩形ABCD中， $A D = 4$ ， $A B = 8$ ，对角线AC，BD相交于点O，点E，F分别为CD，DA延长线上的点，且 $D E = 4$ ， $A F = 2$ ，连接EF，G为EF的中点，连接OE，交AD于点H，连接GH．

(1)、求证：H是OE的中点；

(2)、求GH的长．

查看试题解析
26. 在平面直角坐标系xOy中，一次函数 $y = k x + b (k > 0)$ 的图象与x轴交于点 $A (- 4 ， 0)$ ，与y轴正半轴交于点B，且 $A B = 4 \sqrt{2}$ ．

(1)、求这个一次函数的解析式；

(2)、当 $x = 2$ 时，函数 $y = m x (m \neq 0)$ 的值与一次函数 $y = k x + b (k > 0)$ 的值相等，求m的值；

(3)、当 $x < 2$ 时，对于x的每一个值，函数 $y = n x (n \neq 0)$ 的值小于一次函数 $y = k x + b (k > 0)$ 的值，直接写出n的取值范围．

查看试题解析
27. 在正方形ABCD中，点E在射线BC上（不与点B，C重合），连接DB，DE，过点E在DE的左侧，作 $E F ⊥ D E$ 且使 $E F = D E$ ，连接BF．

(1)、如图1，点E在BC边上．
①依题意补全图1；
②求证： $\sqrt{2} B E = B D - B F$ ；

(2)、如图2，点E在BC边的延长线上，直接用等式表示线段BD，BE，BF之间的数量关系．

查看试题解析
28. 对于平面直角坐标系xOy中的点P和四边形OABC，给出如下定义：若在四边形OABC上存在一点Q，使得P，Q两点间的距离小于或等于1，则称P为四边形OABC的“关联点”．
如图，已知点 $A (\sqrt{3} ， 3)$ ， $B (2 \sqrt{3} ， 0)$ ， $C (\sqrt{3} ， - 3)$ ．

(1)、在点 $D (0 ， 2)$ ， $E (3 ， - 2)$ ， $F (5 ， 3)$ 中，四边形OABC的关联点是；

(2)、点G为直线 $l ： y = k x - (\sqrt{3} k - 5) (k \neq 0)$ 上一点．
①若直线 $l ： y = k x - (\sqrt{3} k - 5) (k \neq 0)$ 过点 $D (0 ， 2)$ ，点G是四边形OABC的关联点，求点G的横坐标的取值范围；
②若直线 $l ： y = k x - (\sqrt{3} k - 5) (k \neq 0)$ 上，不存在点G是四边形OABC的关联点，直接写出k的取值范围．

查看试题解析

离开学校的时间/h	0.1	0.5	0.8	1	3
离学校的距离/km	2	10		12

	甲	乙	丙	丁
平均分	94	94	92	92
方差	23	35	23	35