安徽省阜阳市临泉县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 若二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列计算中,正确的是( )A、 B、 C、 D、3. 关于x的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数由m的值确定4. 用配方法解方程时,结果正确的是( )A、 B、 C、 D、5. 疫情期间,某商店连续7天销售口罩的盒数分别为10,12,14,13,12,12,11.关于这组数据,以下结论错误的是( )A、众数是12 B、平均数是12 C、中位数是12 D、方差是6. 如图, , ,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
 A、 B、 C、 D、7. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC8. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、 B、 C、 D、7. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC8. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、59. 如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形 (相邻纸片之间不重叠,无缝隙).若四边形 的面积为13,中间空白处的四边形 的面积为1,直角三角形的两条直角边分别为 和 ,则 ( )
A、2 B、3 C、4 D、59. 如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形 (相邻纸片之间不重叠,无缝隙).若四边形 的面积为13,中间空白处的四边形 的面积为1,直角三角形的两条直角边分别为 和 ,则 ( )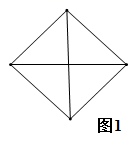
 A、12 B、13 C、24 D、2510. 如图,在边长为3的正方形 中, , ,则 的长是( )
A、12 B、13 C、24 D、2510. 如图,在边长为3的正方形 中, , ,则 的长是( )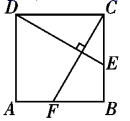 A、1 B、 C、 D、2
A、1 B、 C、 D、2二、填空题
-
11. 计算: .12. 若一元二次方程无实数根,则的取值范围是 .13. 在中, , 若E为的中点,则 .14. 如图,折叠矩形纸片ABCD,使点B的对应点E落在CD边上,GH为折痕,已知 , .
①当点E恰好落在CD边的中点上时,线段BH的长为 .
②当折痕GH最长时,线段BH的长为 .

三、解答题
-
15. 计算:16. 解方程: .17. 已知: , 求代数式值18. 如图,已知 , 平分 , 且 , 作AD的垂直平分线交AC于点F,作 , 求的周长.
 19. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根分别为 、 ,且 ,求 的值.20. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.21. 某校在一次历史考试中,随机抽取了九年级(1)班部分学生的成绩(单位:分)并根据统计结果绘制成了如图所示的两幅不完整的统计图,其中成绩在70~80分的学生人数与成绩在90~100分的学生人数之比为6:7,请结合图中的信息回答下列问题:
19. 已知关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根分别为 、 ,且 ,求 的值.20. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.21. 某校在一次历史考试中,随机抽取了九年级(1)班部分学生的成绩(单位:分)并根据统计结果绘制成了如图所示的两幅不完整的统计图,其中成绩在70~80分的学生人数与成绩在90~100分的学生人数之比为6:7,请结合图中的信息回答下列问题: (1)、本次共抽取学生人;(2)、补全条形统计图;(3)、该校九年级学生共有2400人,请你估计成绩在50~70分的人数有多少人.
(1)、本次共抽取学生人;(2)、补全条形统计图;(3)、该校九年级学生共有2400人,请你估计成绩在50~70分的人数有多少人.