安徽省安庆市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 如果是二次根式,那么x应满足( )A、x≥2 B、x>2 C、x≤2 D、x<22. 下列计算正确的是( )A、 B、 C、 D、3. 关于x的一元二次方程x2+kx-1=0的根的情况是( )A、有两个不相等的同号实数根 B、有两个不相等的异号实数根 C、有两个相等的实数根 D、没有实数根4. 在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差S甲2=1.21,乙的成绩的方差S乙2=3.98,由此可知( ).
A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定5. 下列哪一个角度可以作为一个多边形的内角和( )A、 B、 C、 D、6. 平行四边形中一边长为10cm,那么它的两条对角线长度可以是( )A、8cm和10cm B、6cm和10cm C、6cm和8cm D、10cm和12cm7. 在菱形ABCD中, , , 求平行线AB与CD之间的距离为( )A、 B、 C、 D、8. 有五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )A、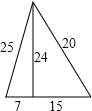 B、
B、 C、
C、 D、
D、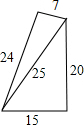 9. 如图,在矩形中,边的长为3,点 , 分别在 , 上,连接 , , , . 若四边形是菱形,且 , 则边的长为( )
9. 如图,在矩形中,边的长为3,点 , 分别在 , 上,连接 , , , . 若四边形是菱形,且 , 则边的长为( ) A、 B、 C、 D、10. 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE= AB2 . 其中正确的有( )
A、 B、 C、 D、10. 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE= AB2 . 其中正确的有( )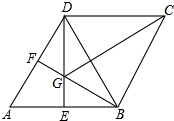 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在 , , 中,与是同类二次根式的是 .12. 若方程有两个相等的根,则方程的根分别是 .13. 如图所示,在边长为的正方形中,点为边的中点,点为对角线上一动点,连接、 , 则周长最小值为 .
 14. 如图,将一个长为8,宽为4的矩形纸片先从下向上,再从左向右对折两次后,沿过所得矩形较长一边中点的直线剪掉一部分,再将剩下的打开,得到一个正方形,则这个正方形的面积是 .
14. 如图,将一个长为8,宽为4的矩形纸片先从下向上,再从左向右对折两次后,沿过所得矩形较长一边中点的直线剪掉一部分,再将剩下的打开,得到一个正方形,则这个正方形的面积是 .
三、解答题
-
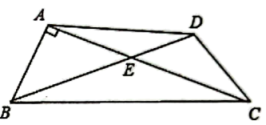
15. 化简: .16. 用配方法解方程:2 +1=317. 如果关于的一元二次方程有两个实数根、 , 且 , 求的值.18. 如图,在四边形中,对角线 , 交于点 , , , , , . 求的长和四边形的面积.
 19. 一款服装每件进价为80元,销售价为120元时,每天可售出20件,为了扩大销售量,增加利润,经市场调查发现,如果每件服装降价1元,那么平均每天可多售出2件.(1)、每件服装降价多少元时,能让利于顾客并且商家平均每天能赢利1200元.(2)、商家能达到平均每天赢利1800元吗?请说明你的理由.20. 如图所示:已知是等边三角形,点、分别在线段 , 上, , .
19. 一款服装每件进价为80元,销售价为120元时,每天可售出20件,为了扩大销售量,增加利润,经市场调查发现,如果每件服装降价1元,那么平均每天可多售出2件.(1)、每件服装降价多少元时,能让利于顾客并且商家平均每天能赢利1200元.(2)、商家能达到平均每天赢利1800元吗?请说明你的理由.20. 如图所示:已知是等边三角形,点、分别在线段 , 上, , .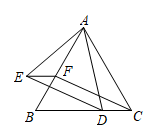 (1)、求证:四边形是平行四边形;(2)、若 , 求证 .21. 在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点.
(1)、求证:四边形是平行四边形;(2)、若 , 求证 .21. 在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点.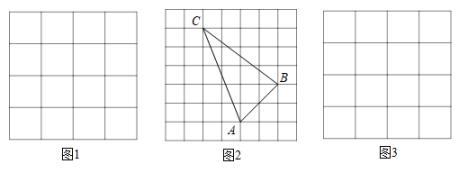 (1)、在图1中,以格点为顶点画 , 使三边长分别为、、;(2)、如图2,各顶点均在格点上,求的面积和点到的距离;(3)、在图3中,以格点为顶点画直角边长为无理数的等腰直角三角形,并说明理由.22. 某公司员工某月工资表如下:
(1)、在图1中,以格点为顶点画 , 使三边长分别为、、;(2)、如图2,各顶点均在格点上,求的面积和点到的距离;(3)、在图3中,以格点为顶点画直角边长为无理数的等腰直角三角形,并说明理由.22. 某公司员工某月工资表如下:员工
总经理
副经理
职员
职员
职员
职员
职员
职员
职员
每月工资(元)
24000
16000
4800
4400
6800
5200
4400
2000
4400
该公司三位职员对收入情况作出如下评价:
甲:我的月工资是4800元,在公司中算中等收入;
乙:我们好几个人的月工资都是4400元;
丙:我们公司员工收入很高,月工资为8000元.
请你用所学知识回答下列问题:
(1)、甲所说的数据4800元,我们称之为该组数据的;(填平均数、众数或中位数)(2)、乙所说的数据4400元,我们称之为该组数据的;(填平均数、众数或中位数)(3)、丙是用什么方法得出8000元的?(4)、丙的说法能否反映该公司职员收入的一般水平,为什么?23.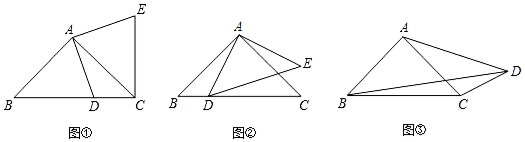 (1)、问题:如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为;(2)、探索:如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;(3)、应用:如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
(1)、问题:如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为;(2)、探索:如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;(3)、应用:如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.