陕西省西北农林科大附高2021-2022学年高二下学期理数期末考试试卷

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、选择题（本大题共12个小题，每小题5分，共60分．）

1. 将6封信投入4个邮筒，且6封信全部投完，不同的投法有（）

A、 $4^{6}$ 种 B、 $6^{4}$ 种 C、4种 D、24科

查看试题解析
2. 掷两枚质地均匀的骰子，设A＝“第一枚出现奇数点”，B＝“第二枚出现偶数点”，则A与B的关系为（）

A、互斥 B、互为对立 C、相互独立 D、相等

查看试题解析
3. 从字母a，b，c，d，c，f中选出4个字母排成一列，其中一定要选出a和b，并且必须相邻（a在b的前面），共有排列方法（）

A、36种 B、72种 C、90种 D、144种

查看试题解析
4. 已知一个线性回归方程为 $\hat{y}$ =1.5x+45，其中x的取值依次为1，7，5，13，19，则 $\bar{y}$ =（）

A、58.5 B、46.5 C、60 D、75

查看试题解析
5. 已知离散形随机变量X的分布列如下：

X

1

3

5

P

0.5

m

0.2

则其均值EX等于（）

A、1 B、0.6 C、 $2 + 3 m$ D、2.4

查看试题解析
6. 下列关于 ${(a - b)}^{11}$ 的说法中错误的是（）

A、展开式中的二项式系数之和为2048 B、展开式各项系数之和为0 C、展开式中只有第6项的二项式系数最大 D、展开式中第6项的系数最小

查看试题解析

7. 假设有两个分类变量X与Y，它们可能的取值分别为

{x_{1} ， x_{2}}

和

{y_{1} ， y_{2}}

，其2×2列联表如下：

	$y_{1}$	$y_{2}$	总计
$x_{1}$	a	b	a＋b
$x_{2}$	c	d	c＋d
总计	a＋c	b＋d	a＋b＋c＋d

以下各组数据中，对于同一样本能说明x与y有关系的可能性最大的一组为（）

A、a＝5，b＝4，c＝3，d＝2 B、a＝5，b＝3，c＝4，d＝2 C、a＝2，b＝3，c＝4，d＝5 D、a＝2，b＝3，c＝5，d＝4

查看试题解析

8. 若 $P (ξ ⩽ n) = 1 - a ， P (ξ ⩾ m) = 1 - b$ ，其中 $m < n$ ，则 $P (m \leq ξ \leq n)$ 等于（）

A、 $1 - a - b$ B、 $2 - a - b$ C、 $a + b - 1$ D、 $a + b - 2$

查看试题解析
9. 某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）

A、0.8 B、0.75 C、0.6 D、0.45

查看试题解析
10. 在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C为正态分布N（0，1）的密度曲线）的点的个数的估计值为（）

A、2386 B、2718 C、3413 D、4772

查看试题解析
11. 某次国际象棋比赛规定，胜一局得3分，平一局得1分，负一局得0分，某参赛队员比赛一局胜的概率为a，平局的概率为b，负的概率为c（ $a ， b ， c \in [0 ， 1)$ ），已知他比赛一局得分的数学期望为1，则ab的最大值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{12}$ C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析
12. 已知 $C_{n}^{0} + 3 C_{n}^{1} + 3^{2} C_{n}^{2} + 3^{3} C_{n}^{3} + \dots + 3^{n} C_{n}^{n} = 1024$ ，则 $C_{n}^{1} + C_{n}^{2} + \dots + C_{n}^{n}$ 的值等于（）

A、31 B、32 C、63 D、64

查看试题解析

二、填空题（本大题共4个小题，每小题5分，共20分）

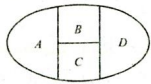
13. $77^{77} - 7$ 被19除所得的余数是．

查看试题解析
14. 已知随机变量X服从二项分布B（n，p）．若 $E X = 30$ ， $D X = 20$ ，则p＝．

查看试题解析
15. 4名不同科目的实习教师被分配到三个班级，每班至少有一人的不同分法有种．

查看试题解析
16. 如图，用6种不同的颜色给图中A、B、C、D四块区域涂色，若相邻区域不能涂同一种颜色，则不同的涂法共有种．

查看试题解析

三、解答题（本大题共6个小题，共70分）

17. 吃零食是中学生中普遍存在的现象，吃零食对学生身体发育有诸多不利影响，影响学生的健康成长，下表是性别与吃零食的列联表：

	男	女	总计
喜欢吃零食	5	12	17
不喜欢吃零食	40	28	68
总计	45	40	85

请问喜欢吃零食与性别是否有关？

查看试题解析

18. 3名男同志和3名女同志到4辆不同的公交车上服务．

(1)、若每辆车上都要有人服务，但最多安排男女各一名，有多少种不同的安排方法？

(2)、若男女各包两辆车，有多少种安排方法？

查看试题解析
19. 已知 ${(2 x - 3)}^{7} = a_{0} {(x - 1)}^{7} + a_{1} {(x - 1)}^{6} + \dots + a_{6} (x - 1) + a_{7}$ ．

(1)、求 $a_{0} + a_{1} + a_{2} + \dots + a_{7}$ ；

(2)、求 $a_{0} - a_{7}$ ．

查看试题解析
20. 现有7位同学（分别编号为A，B，C，D，E，F，G）排成一排拍照，若其中A，B，C三人互不相邻，D，E两人也不相邻，而F，G两人必须相邻，求不同的排法总数．

查看试题解析
21. 某银行柜台设有一个服务窗口，假设顾客办理业务所需的时间互相独立，且都是整数分钟，对以往顾客办理业务所需的时间统计结果如表：

办理业务所需的时间（分）

1

2

3

4

5

频率

0.1

0.4

0.3

0.1

0.1

从第一个顾客开始办理业务时计时．

(1)、估计第三个额客恰好等待4分钟开始办理业务的概率；

(2)、X表示至第2分钟末已办理完业务的顾客人数，求X的分布列及数学期望．

查看试题解析
22. 根据国际疫情形势以及传染病防控的经验，加快新冠病毒疫苗接种是当前有力的防控手段．我国正在安全、有序加快推进疫苗接种工作，某乡村采取通知公告、微信推送、广播播放、条幅宣传等形式，积极开展疫苗接种社会宣传工作，消除群众疑虑，提高新冠疫苗接种率，让群众充分地认识到了疫苗接种的重要作用，自宣传开始后村干部统计了本村200名居民（未接种）⁵天内每天新接种疫苗的情况，得如下统计表：

第x天

1

2

3

4

5

新接种人数y

10

15

19

23

28

(1)、建立y关于x的线性回归方程；

(2)、预测该村第几天当日居民新接种人数首次超过35人？

查看试题解析

办理业务所需的时间（分）	1	2	3	4	5
频率	0.1	0.4	0.3	0.1	0.1

X	1	3	5
P	0.5	m	0.2

第x天	1	2	3	4	5
新接种人数y	10	15	19	23	28