四川省成都市高新技术产业开发区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-07-26 类型：期末考试

进入出卷网下载

一、选择题

1. 简简单单的七巧板能拼出千变万化的图形．殊不知七巧板作为中国传统玩具在国外也甚为流传，被称为“唐图”．下面四幅七巧板拼图的形状是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{2 x - 1}{3 x + 2}$ 的值为0，则x的值是（）

A、2 B、1 C、 $\frac{1}{2}$ D、 $- \frac{2}{3}$

查看试题解析
3. 已知 $x > y$ ，则下列不等式一定成立的是（）

A、 $x - 6 < y - 6$ B、 $- 2 x < - 2 y$ C、 $2 x - 1 < 2 y - 1$ D、 $a^{2} x > a^{2} y$

查看试题解析
4. 一个多边形的内角和等于它的外角和的2倍，则该多边形的边数是（）

A、五 B、六 C、七 D、八

查看试题解析
5. 在平面直角坐标系 $x O y$ 中，将点 $A (4 ， - 2)$ 先向左平移2个单位，再向上平移4个单位得点B，则点B的坐标是（）

A、 $(2 ， 2)$ B、 $(2 ， - 6)$ C、 $(6 ， 2)$ D、 $(6 ， - 6)$

查看试题解析
6. 一个菱形ABCD 的周长为40cm，它的一条对角线长10cm，则下列关于该菱形的说法错误的是（）

A、另一条对角线长为 $10 \sqrt{3}$ cm B、有一组对角的大小为60° C、面积为 $100 \sqrt{3} {cm}^{2}$ D、任意一边上的高均为 $5 \sqrt{3}$ cm

查看试题解析
7. 下列从左至右的变形，属于因式分解的是（）

A、 $x^{2} + 2 x + 2 = {(x + 1)}^{2} + 1$ B、 $- x^{2} + y^{2} = (- x + y) (- x - y)$ C、 $x^{2} - x + \frac{1}{4} = {(x - \frac{1}{2})}^{2}$ D、 $4 x y^{2} - 4 x^{2} y = x y (4 y - 4 x)$

查看试题解析
8. 如图，点E是矩形ABCD边AD上一动点，连接BE，以BE边作矩形BEFG，使得FG始终经过点C．若矩形ABCD的面积为 $s_{1}$ ，矩形BEFG的面积为 $s_{2}$ ，则 $s_{1}$ 与 $s_{2}$ 的大小关系是（）

A、 $s_{1} < s_{2}$ B、 $s_{1} = s_{2}$ C、 $s_{1} > s_{2}$ D、不确定

查看试题解析

二、填空题

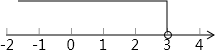
9. 一个不等式的解集如图所示，则这个不等式的正整数解是.

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 60 °$ ，CD是 $△ A B C$ 的高，且 $B D = 1$ ，则AD的长是

查看试题解析
11. 如图，线段AB的端点B在直线MN上，过线段AB上的一点O作MN的平行线，分别交 $∠ A B M$ 和 $∠ A B N$ 的平分线于点C，D，连接AC，AD．添加一个适当的条件：当时，四边形ACBD为矩形．

查看试题解析
12. 已知，在平面直角坐标系 $x O y$ 中，一次函数 $y = m x + 3 - m$ 的图象经过第一、二、三象限，则m的取值范围是

查看试题解析
13. 如图，在 $△ A B C$ 中，分别以B，C为圆心，大于 $\frac{1}{2} B C$ 的长为半径，在BC两侧画弧，分别交于E、F两点，连接EF，并延长EF，交AB于点D．若 $B D = 4$ ， $A D = 3$ ，且 $∠ B = 45 °$ ，则AC的长为

查看试题解析
14. 某工人师傅要制作一个底面为正方形的无盖长方体盒子，他在一块边长为a的正方形铁皮的四个角，各剪去一个边长为b（ $a > b$ ），如图所示，若 $a = 3.6$ ， $b = 0.8$ ，则剩余部分的面积是．

查看试题解析
15. 关于y的方程 $\frac{y + a}{y - 1} + \frac{2 a}{1 - y} = 2$ 的解为非负数，则a的取值范围是．

查看试题解析
16. 如图，菱形ABCD的对角线AC与BD交于点O，点E是AD边上一点，且 $O D = O E$ ．若 $A C = 8$ ， $B D = 6$ ，则AE的长是．

查看试题解析
17. 如图，矩形ABCD在平面直角坐标系中，已知 $A (0 ， 3)$ ， $C (4 ， 0)$ ，点P为射线AB上一动点，将直线OP绕点P逆时针旋转90°，交直线BC于点Q，当 $△ O P Q$ 为等腰三角形时，点P的坐标为．

查看试题解析
18. 如图，在边长为2的正方形ABCD中，点E，F分别是边BC，AD上的点，连接EF，将四边形ABEF沿EF折叠，点B的对应点G恰好落在CD边上，点A的对应点为H，连接BH．则 $B H + E F$ 的最小值是．

查看试题解析

三、解答题

19.

(1)、解不等式： $1 - \frac{7 x - 1}{8} > \frac{3 x - 2}{4}$ ；

(2)、解方程： $\frac{x - 2}{2 x - 1} + 1 = \frac{3}{2 - 4 x}$ ．

查看试题解析
20. 端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元，某商家在节前用8000元购进猪肉粽和6000元购进的豆沙粽盒数相同．

(1)、每盒豆沙粽和每盒猪肉粽的进价分别是多少元？

(2)、商家计划在销售过程中，将猪肉粽的售价定为在进价的基础上提高25%，豆沙粽的售价定为每盒36元，进行销售，且按上述定价两种各售出了a盒后，将剩余的粽子均打九折出售．若要使得所有粽子售完且商家获利不低于2800元，则a的最小值是多少？

查看试题解析
21. 先化简： $\frac{a - 1}{a + 1} \div (a - \frac{3 a - 1}{a + 1})$ ，再任选一个你喜欢的数a代入求值．

查看试题解析
22. 已知一次函数 $y_{1} = a x + b$ 的图象分别交x轴和y轴于B，D两点，另一个一次函数 $y_{2} = b x + a$ 的图象分别交x轴和y轴于C，E两点，且两个函数的图象交于点 $A (1 ， 4)$ ．

(1)、当a，b为何值时， $y_{1}$ 与 $y_{2}$ 的图象重合；

(2)、当 $D E = 2$ 时，求 $△ A B C$ 的面积；

(3)、当 $0 < a < 4$ ，且使得 $x < 1$ 时，始终有 $y_{1} > y_{2}$ ，求b 取值范围．

查看试题解析
23. 如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上，连接AB，AC，并按下列要求用无刻度的直尺作图，并保留作图痕迹．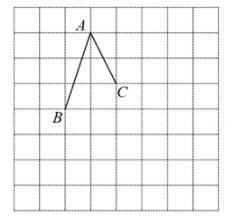

（1）将线段AB沿AC方向平移 $\sqrt{5}$ 个单位长度得线段CD，并连接BD；
（2）将点C绕点A逆时针旋转90°，使点C落在点E处，并作一条直线l，使其过点E并且平分四边形ABDC的面积．

查看试题解析
24. 【数学初探】
在数学课上，叶老师提出了一个探究型问题：“如图1，你能借助锐角 $△ A B C$ 画出一个菱形，使 $∠ A$ 为该菱形的一个内角吗？”雷同学提出了自己的见解：如图2，①作 $∠ B A C$ 的平分线AE，交BC于点E；②作AE的中垂线l分别交AB、AC、AE于点F、G、H；③连接EF，EG，则四边形AFEG是菱形．

(1)、请你帮助雷同学证明四边形AFEG是菱形．

(2)、【深入探究】

雷同学开启大胆尝试，如图3，将 $△ A B C$ 的中线BO延长至点D，使 $D O = O B$ ，连接AD，CD，平移图2中的直线l（平移过程中直线l与AB、AC、AE的交点仍为F、G、H），当直线l恰好经过点D时，他通过测量发现了线段OG与线段BF存在特定的数量关系．
请你写出线段OG与线段BF的数量关系，并求证．

(3)、【迁移应用】
如图4，在（2）的条件下，若 $∠ B A C = 60 °$ ，且 $\frac{S_{△ D O G}}{S_{△ D B F}} = \frac{3}{8}$ 时，求 $\frac{A D}{A B}$ 的值．

查看试题解析
25. 如图，在四边形ABCD中，E，G两点分别是边AB，CD的中点，F，H两点分别是对角线BD，AC的中点，连接EF，FG，GH，HE．

(1)、若 $A D = B C$ 时，求证：四边形EFGH是菱形；

(2)、添加适当的条件，使四边形EFGH是矩形，并证明．

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，已知一次函数 $y = x + m$ 的图象与x轴、y轴的交点分别为A，B，与一次函数 $y = - 3 x + n (n > m)$ 的图象交于点P，又一次函数 $y = - 3 x + n$ 的图象与x轴、y轴的交点分别为C，D．

(1)、直接写出 $∠ P A C$ 的度数并用含m，n的代数式表示点P的坐标；

(2)、若 $S_{△ A B O} = S_{△ B D P}$ ，且四边形BOCP 面积为4，求这两个一次函数的表达式；

(3)、在（2）的条件下，直线AB上点M及平面内一点N，恰好使得以D，P，M，N为顶点的四边形是菱形，请直接写出点N的坐标．

查看试题解析