浙江省绍兴市越城区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-26 类型:期末考试
一、选择题(本大题共10小题,每题3分,共30分)
-
1. 化简 的结果是( )A、2 B、2 C、4 D、102. 平行四边形ABCD中,∠A+∠C=140°,那么∠B的度数是( )A、80° B、90° C、100° D、110°3. 已知x=﹣1是方程x2+ax+2=0的一个根,则a的值为( )A、﹣1 B、1 C、﹣3 D、34. “红色小讲解员”演讲比赛中,7位评委分别给某位选手打出“原始分”.按照比赛规则,评定该选手成绩采用是“有效分”,即从7个“原始分”中去掉一个最高分和一个最低分,得到5个数据为“有效分”.那么5个“有效分”与7个“原始分”这两组数据相比,相等的一个量是( )A、中位数 B、众数 C、平均数 D、方差5. 对函数y= 的描述错误的是( )A、图象过点(1,1) B、图象在第一、三象限 C、当x<1时,y>1 D、y随x的增大而减小6. 如图,在菱形ABCD中,对角线AC、BD相较于点O,BD=8,BC=5,AE⊥BC于点E,则AE的长为( )
 A、 B、 C、 D、7. 已知n是一个正整数,若 是整数,则n的最小值是( )A、3 B、5 C、15 D、258. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
A、 B、 C、 D、7. 已知n是一个正整数,若 是整数,则n的最小值是( )A、3 B、5 C、15 D、258. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )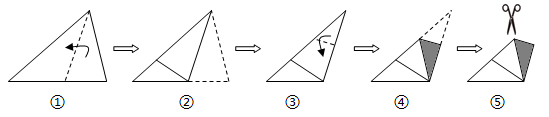 A、等腰三角形 B、直角三角形 C、矩形 D、菱形9. 如图,点A是反比例函数y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣ 的图象于点B,以AB为边作▱ABCD,其中C、D在x轴上,则S▱ABCD为( )
A、等腰三角形 B、直角三角形 C、矩形 D、菱形9. 如图,点A是反比例函数y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣ 的图象于点B,以AB为边作▱ABCD,其中C、D在x轴上,则S▱ABCD为( ) A、2.5 B、3 C、5 D、610. 已知某四边形ABCD的两条对角线AC、BD相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( )
A、2.5 B、3 C、5 D、610. 已知某四边形ABCD的两条对角线AC、BD相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( ) A、
A、 B、
B、 C、
C、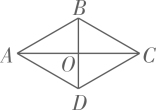 D、
D、
二、填空题(本大题共6小题,每题3分,共18分)
-
11. 根式 中字母x的取值范围是 .12. 如果一个八边形的每一个内角都相等,那么它的一个内角的度数等于 .13. 已知关于x的一元二次方程x2﹣6x+2m﹣1=0有两个相等的实数根,那么这个两个相等的实数根为 .14. 由5个整数组成的一组数据,中位数为4,将它们从小到大排列,如果排列后这组数据的众数是6,那么这5个整数的和最大是 .15. 如图,在菱形ABCD中,∠ABC=30°,连结AC,按以下步骤作图:分别以点C,B为圆心,以BC的长为半径作弧,两弧相交于点P,连结BP与CP,则∠ACP的度数为 .
 16. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .
16. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .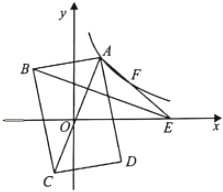
三、解答题(本大题共52分)
-
17.(1)、计算: (3﹣ )﹣ +| ﹣2|;(2)、解方程:x2﹣4x=2.18. 如图均是由边长为1的小正方形拼成的网格,每个小正方形的顶点称为格点,点P、Q、R均在格点上.要求只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法.
 (1)、如图1,以线段PQ为对角线画一个面积为9的平行四边形PMQN,且M、N在格点上;(2)、如图2,画△PQR边RQ上的高线PH,点H是垂足.19. 一商店销售某品牌的体恤衫,平均每天可售出20件,每件盈利40元在“618活动”期间该店采取了降价促销,在每件盈利不少于25元的前提下,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,那么平均每天可销售多少件?(2)、当每件体恤衫的售价降价多少元时,该商店每天销售利润为1200元?20. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作EF⊥AC,分别交AB,DC于点E,F,连接AF,CE.
(1)、如图1,以线段PQ为对角线画一个面积为9的平行四边形PMQN,且M、N在格点上;(2)、如图2,画△PQR边RQ上的高线PH,点H是垂足.19. 一商店销售某品牌的体恤衫,平均每天可售出20件,每件盈利40元在“618活动”期间该店采取了降价促销,在每件盈利不少于25元的前提下,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,那么平均每天可销售多少件?(2)、当每件体恤衫的售价降价多少元时,该商店每天销售利润为1200元?20. 如图,▱ABCD的对角线AC,BD相交于点O,过点O作EF⊥AC,分别交AB,DC于点E,F,连接AF,CE. (1)、若OE= ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.21. 甲乙两人在相同的条件下各射击10次,每次射击的成绩情况如图所示.(方差的计算公式:s2= [(x1﹣ )2+(x2﹣ )2+……+(xn﹣ )2].)
(1)、若OE= ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.21. 甲乙两人在相同的条件下各射击10次,每次射击的成绩情况如图所示.(方差的计算公式:s2= [(x1﹣ )2+(x2﹣ )2+……+(xn﹣ )2].) (1)、请你填写甲的相关数据:
(1)、请你填写甲的相关数据:平均数
众数
方差
甲
(2)、如果甲第11次射击的成绩是8环,则甲得分中的三个统计量,即平均数、众数、方差发生哪些变化?(3)、根据甲、乙10次射击的成绩,如果教练选择甲参加射击比赛,教练的理由是什么?如果教练选择乙参加射击比赛,教练的理由又是什么?22. 如图,在菱形ABCD中,AB=10,S菱形ABCD=60,点E从点B出发在边BC上向终点C运动.过点E作边BC的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.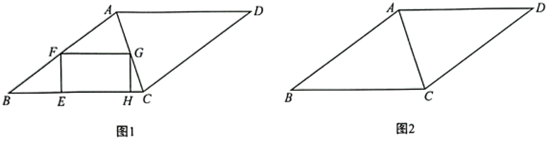 (1)、如图1,点G在AC上.
(1)、如图1,点G在AC上.①求证:FA=FG;
②若点G是AC的中点,求证:BF=FG;
(2)、若EF=FG,当EF过AC中点时,求AG的长.23. 已知点A(3,2)、点B(m,n)在反比例函数y= (x>0)图象上,点C是x轴上的一个动点. (1)、求k的值;(2)、若m=1,C(﹣1,0),试判断△ABC的形状,并说明理由;(3)、若点C在x轴正半轴上,当△ABC为等腰直角三角形时,求出点C的坐标.
(1)、求k的值;(2)、若m=1,C(﹣1,0),试判断△ABC的形状,并说明理由;(3)、若点C在x轴正半轴上,当△ABC为等腰直角三角形时,求出点C的坐标.