浙江省杭州市八县区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-26 类型:期末考试
一、选择题(本大题共10小题,共30分)
-
1. 下列与杭州亚运会有关的图案中,中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 某小组4名同学的英语口试成绩依次为27,23,25,29,这组数据的中位数是( )A、24 B、25 C、26 D、274. 若一元二次方程 有两个相等的实数根,则 的值是( )A、-1 B、1 C、2 D、45. 如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 已知y是关于x的反比例函数, , 和 , 是自变量与函数的两组对应值.则下列关系式中,成立的是( )A、 B、 C、 D、7. 对于命题“在同一平面内,若 , ,则 ”,用反证法证明,应假设( )A、 B、 C、 与 相交 D、 与 相交8. 2020年北京冬奥会吉祥物“冰墩墩”敦厚可爱,深受大家欢迎.某生产厂家1月份平均日产量为20000个,随着冬奥会的举行,“冰墩墩”一路走红,供不应求.为满足市场需求,工厂决定扩大产能,3月份平均日产量达到33800个,设1至3月份冰墩墩日产量的月平均增长率为 ,则可列方程为( )A、 B、 C、 D、9. 已知点 , , 都在反比例函数 的图象上,则( )A、 B、 C、 D、10. 如图,矩形中, , , 点E,F,G,H分别在矩形各边上,且四边形为平行四边形,则平行四边形周长的最小值为( )
2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 某小组4名同学的英语口试成绩依次为27,23,25,29,这组数据的中位数是( )A、24 B、25 C、26 D、274. 若一元二次方程 有两个相等的实数根,则 的值是( )A、-1 B、1 C、2 D、45. 如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 已知y是关于x的反比例函数, , 和 , 是自变量与函数的两组对应值.则下列关系式中,成立的是( )A、 B、 C、 D、7. 对于命题“在同一平面内,若 , ,则 ”,用反证法证明,应假设( )A、 B、 C、 与 相交 D、 与 相交8. 2020年北京冬奥会吉祥物“冰墩墩”敦厚可爱,深受大家欢迎.某生产厂家1月份平均日产量为20000个,随着冬奥会的举行,“冰墩墩”一路走红,供不应求.为满足市场需求,工厂决定扩大产能,3月份平均日产量达到33800个,设1至3月份冰墩墩日产量的月平均增长率为 ,则可列方程为( )A、 B、 C、 D、9. 已知点 , , 都在反比例函数 的图象上,则( )A、 B、 C、 D、10. 如图,矩形中, , , 点E,F,G,H分别在矩形各边上,且四边形为平行四边形,则平行四边形周长的最小值为( )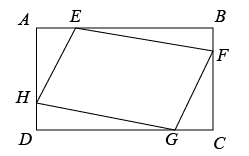 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24分)
-
11. 计算: = .12. 下表记录了甲、乙、丙、丁四名跳远运动员10次选拔赛成绩数据信息.要根据表中的信息选择一名成绩好又发挥稳定的运动员参加比赛,应该选择的运动员是 .
甲
乙
丙
丁
平均数
562
559
562
560
方差
3.5
3.5
15.5
16.5
13. 已知关于x的一元二次方程有一个根为-2,则.14. 已知 , , 则的值是.15. 如图,点 , , , 为正方形 四边中点,连结 , , , 若 ,则四边形 的面积是.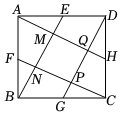 16. 反比例函数y= ,当1≤x≤3时,函数y的最大值和最小值之差为4,则k=.
16. 反比例函数y= ,当1≤x≤3时,函数y的最大值和最小值之差为4,则k=.三、解答题(本大题共7小题,共66分)
-
17.(1)、计算: .(2)、解方程: .18. 在探究欧姆定律时,小明发现小灯泡电路上的电压保持不变,通过小灯泡的电流越大,灯就越亮.设选用小灯泡的电阻为 , 通过的电流强度为.(1)、若电阻为 , 通过的电流强度为 , 求I关于R的函数表达式.(2)、如果电阻小于 , 那么与原来的相比,小灯泡的亮度将发生什么变化?19. 某公司要招聘一名职员,根据实际需要,从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行了测试,测试成绩如表.
项目
应聘者
甲
乙
丙
学历
9
8
8
经验
8
6
9
能力
7
8
8
态度
5
7
5
(1)、如果将学历、经验、能力和态度四项得分按1:1:1:1的比例确定每人的最终得分,并以此为依据确定录用者,那么谁将被录用?(2)、如果你是这家公司的招聘者,请按你认为的各项“重要程度”设计四项得分的比例,以此为依据确定录用者,并说一说你这样设计比例的理由.20. 已知:如图,点 ,点 是▱ 的对角线 上的两点,且 .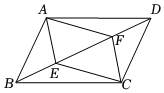 (1)、求证: .(2)、求证:四边形 是平行四边形.21. 某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件.为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量,增加利润.据测算,每件童装每降价1元,平均每天可多售出2件.设每件童装降价x元.(1)、每天可销售多少件,每件盈利多少元?(用含的代数式表示)(2)、每件童装降价多少元时,平均每天盈利1200元.(3)、平均每天盈利能否达到2000元,请说明理由.22. 对于函数 ,小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.
(1)、求证: .(2)、求证:四边形 是平行四边形.21. 某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件.为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量,增加利润.据测算,每件童装每降价1元,平均每天可多售出2件.设每件童装降价x元.(1)、每天可销售多少件,每件盈利多少元?(用含的代数式表示)(2)、每件童装降价多少元时,平均每天盈利1200元.(3)、平均每天盈利能否达到2000元,请说明理由.22. 对于函数 ,小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.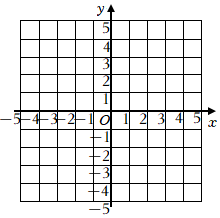 (1)、自变量 的取值范围是.
(1)、自变量 的取值范围是.-1
0
1
3
4
5
-2
-3
-6
6
3
2
(2)、根据列表计算的部分对应值,在平面直角坐标系中用描点法画出该函数的图象.(3)、从中心对称和轴对称的角度分析图象特征,并说说这个函数的增减性.23. 如图,已知菱形 , ,点 是射线 上的动点,以 为边向右侧作等边 ,连结 .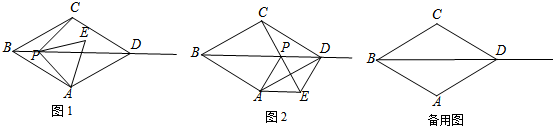 (1)、如图1,点 在线段 上,求证: .(2)、如图2,当 , , 三点共线时,连结 ,求证:四边形 是菱形.(3)、当 时,求 的值.
(1)、如图1,点 在线段 上,求证: .(2)、如图2,当 , , 三点共线时,连结 ,求证:四边形 是菱形.(3)、当 时,求 的值.