湖南省娄底市娄星区2021-2022学年八年级下学期期末考试数学试卷

试卷更新日期：2022-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下列各组数为边长，可以构成直角三角形的是（）

A、2，3，4 B、1，1，2 C、3，3，3 D、1， $\sqrt{5}$ ，2

查看试题解析
3. 若点 $P$ 在第二象限，且点 $P$ 到 $x$ 轴的距离为2，到 $y$ 轴的距离为1，则点 $P$ 的坐标为（）

A、 $(- 1 ， 2)$ B、 $(2 ， 1)$ C、 $(1 ， - 2)$ D、 $(- 2 ， 1)$

查看试题解析
4. 如图所示，公路 $A C$ ， $B C$ 互相垂直，点 $M$ 为公路 $A B$ 的中点，为测量湖泊两侧 $C$ 、 $M$ 两点间的距离，工人师傅测得 $A C = 3 km$ ， $B C = 4 km$ ，则 $M$ ， $C$ 两点间的距离为（） $km$ .

A、 $\frac{5}{2}$ B、3 C、4 D、5

查看试题解析
5. 下列条件中，不能判断四边形是平行四边形的是（）

A、两组对边分别平行 B、一组对边平行，另一组对边相等 C、对角线互相平分 D、一组对边平行，一组对角相等

查看试题解析
6. 下列函数中，是一次函数的是（）

A、 $y = x^{2} + 2$ B、y=3x+1 C、 $y = k x + b$ D、 $y = \frac{3}{x}$

查看试题解析
7. 图，在 $Δ A B C$ 中， $B C = 20$ ， $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点，则 $D E$ 的长度为（）

A、10 B、8 C、6 D、12

查看试题解析
8. 如图， $B D$ 为 $△ A B C$ 的角平分线， $D E ⊥ B C$ 于点E， $D E = 6$ ， $∠ A = 30 °$ ，则 $A D$ 的长为（）

A、6 B、8 C、12 D、16

查看试题解析
9. 如图，菱形ABCD的对角线AC，BD的长分别为6cm，8cm，则这个菱形的周长为（）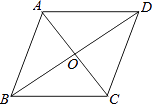

A、5cm B、10cm C、14cm D、20cm

查看试题解析
10. 如图，已知正比例函数 $y_{1} = a x$ 与一次函数 $y_{2} = \frac{1}{2} x + b$ 的图象交于点P.下面有四个结论：① $a < 0$ ；② $b < 0$ ；③当 $x > 0$ 时， $y_{1} < 0$ ；④当 $x < - 2$ 时， $y_{1} < y_{2}$ .其中正确的是（）

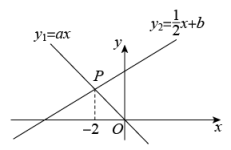A、①② B、②③ C、①③ D、①④

查看试题解析
11. A、B两地相距80km，甲、乙两人沿同一条路从A地到B地， $l_{1}$ 、 $l_{2}$ 分别表示甲、乙两人离开A地的距离 $s (k m)$ 与时间 $t (h)$ 之间的关系，对于以下说法正确的结论是（）

A、乙车出发1.5小时后甲才出发 B、两人相遇时，他们离开A地20km C、甲的速度是 $\frac{80}{3} k m / h$ ，乙的速度是 $\frac{40}{3} k m / h$ D、当乙车出发2小时时，两车相距13km

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ 我们把点 $P (- y + 1 ， x + 1)$ 叫做点 $P$ 的伴随点.已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ ， …这样依次得到点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ， ….若点 $A_{1}$ 的坐标为 $(2 ， 4)$ ，点 $A_{2022}$ 的坐标为（）

A、 $(- 3 ， 3)$ B、 $(- 2 ， - 2)$ C、 $(3 ， - 1)$ D、 $(2 ， 4)$

查看试题解析

二、填空题

13. 已知一个正多边形的一个外角为 $36 °$ ，则这个正多边形的内角和是.

查看试题解析
14. 正比例函数图象经过 $(3, - 6)$ ，则这个正比例函数的解析式是.

查看试题解析
15. 某班按课外阅读时间将学生分为3组，第1、2组的频率分别为0.2、0.5，则第3组的频率是 .

查看试题解析
16. 将函数 $y = - 2 x + 3$ 的图象向下平移2个单位后得到的图象的函数解析式为.

查看试题解析
17. 如图，点E、F分别是正方形 $A B C D$ 的边 $A D$ 、 $C D$ 上的点，且 $O E ⊥ O F$ ，已知 $A D = 6$ ，则图中阴影部分的面积是.

查看试题解析
18. 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），若大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a和b，则 ${(a + b)}^{2}$ 的值为.

查看试题解析

三、解答题

19. 如图所示的正方形网格中，每个小正方形的边长都是1，△ABC顶点都在网格线的交点上，点A坐标为（﹣4，6），点C坐标为（﹣1，4）.

⑴根据上述条件，在网格中建立平面直角坐标系xOy；

⑵画出△ABC分别关于y轴的对称图形△A₁B₁C₁；

⑶请写出点B关于x轴对称点的坐标为▲ .

查看试题解析
20. 如图，在△ABC中，点D是BC边上一点，连接AD，若AB＝10，AC＝17，BD＝6，AD＝8.

(1)、求证：△ABD是直角三角形；

(2)、求BC的长.

查看试题解析

21. 为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试时听写100个汉字，每正确听写出一个汉字得1分，本次决赛学生成绩为

x

（分

)

，且学生决赛成绩的范围是

50

≤

x

＜100，将其按分数段分为五组，绘制成以下不完整表格：

请根据表格提供的信息，解答以下问题：

组别	成绩x分	频数（人数）	频率
一	$50 \leq x < 60$	2	0.04
二	$60 \leq x < 70$	10	0.2
三	$70 \leq x < 80$	14	b
四	$80 \leq x < 90$	a	0.32
五	$90 \leq x < 100$	8	0.16

(1)、求本次决赛共有多少名学生参加；

(2)、直接写出表中

a =

，

b =

；

(3)、请补全相应的频数分布直方图；

(4)、若决赛成绩不低于80分为优秀，求本次大赛的优秀率.

查看试题解析

22. 如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端B离地面0.6m，荡秋千到AB的位置时，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB的长.

查看试题解析
23. 新华书店决定用不多于28000元购进甲乙两种图书共1200本进行销售，已知甲种图书进价是乙种图书每本进价的1.4倍，若用1680元购进甲种图书的数量比用1400元购进的乙种图书的数量少10本，

(1)、甲乙两种图书的进价分别为每本多少元？

(2)、新华书店决定甲种图书售价为每本40元，乙种图书售价每本30元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完）

查看试题解析
24. 如图，在四边形 $A B C D$ 中，AD $∥$ BC， $∠ A B C = ∠ B C D = 90 °$ .对角线 $A C ， B D$ 交于点 $O ， D E$ 平分 $∠ A D C$ 交 $B C$ 于点 $E$ ，连接 $O E$ .

(1)、求证：四边形 $A B C D$ 是矩形；

(2)、若 $C D = 2$ ， $∠ D B C$ = $30 °$ ，求△ $B E D$ 的面积.

查看试题解析
25. 已知：如图一次函数 $y_{1} = k x - 2$ 与 $x$ 轴相交于点 $B (- 2 ， 0)$ ， $y_{2} = x + b$ 与 $x$ 轴相交于点 $C (4 ， 0)$ ，这两个函数图象相交于点A.

(1)、求出k，b的值和点A的坐标；

(2)、连接 $O A$ ，直线 $y_{2} = x + b$ 上是否存在一点 $P$ ，使 $S_{△ O C P} = \frac{1}{3} S_{△ O A C}$ .如果存在，求出点P的坐标；

查看试题解析
26. 如图①，点E是线段AB延长线上一点，且AB＞BE，分别以AB和BE为边作正方形ABCD和BEFG，连接AG，CE.

(1)、请你直接写出AG与CE的数量与位置关系；

(2)、将正方形BEFG绕点B顺时针旋转α（0°＜α＜90°），AG与CE相交于点O，AG与BC相交于点H，BG与CE相交于点M，如图②，请问（1）中AG与CE的数量与位置关系是否成立？若成立，请证明；若不成立，请说明理由；

(3)、连接CG，AE，如图③，若AB＝4，BE＝3，请求出CG²+AE²的值.

查看试题解析