广西壮族自治区梧州市岑溪市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 使 $\sqrt{x - 3}$ 有意义的 $x$ 的取值范围是（）

A、 $x > 3$ B、 $x < 3$ C、 $x \geq 3$ D、 $x \neq 3$

查看试题解析
2. 下列各式中与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $2 \sqrt{3}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
3. 在下列长度的各组线段中，能构成直角三角形的是（）

A、3，4，5 B、7，8，10 C、5，12，14 D、1，1，2

查看试题解析
4. 解方程(x－3)²＝4，最合适的方法是（）

A、直接开平方法 B、配方法 C、公式法 D、因式分解法

查看试题解析
5. 如果正多边形的每个外角等于40°，则这个正多边形的边数是（　　）

A、10 B、9 C、8 D、7

查看试题解析
6. 距考试还有20天的时间，为鼓舞干劲，老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言，小明所在的小组共写了30份留言，该小组共有（）

A、7人 B、6人 C、5人 D、4人

查看试题解析
7. 如图，DE是△ABC的中位线，若BC＝8，则DE的长为（）

A、2 B、4 C、6 D、8

查看试题解析
8. 甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如表：

选手

甲

乙

丙

丁

方差（环²）

0.035

0.016

0.022

0.025

则这四个人种成绩发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 方程x²－4x－5＝0的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判定

查看试题解析
10. 某校团委组织团员开展“百年党史”知识竞赛，九（1）班6位参赛同学成绩为：83，87，80，83，88，83.则以下说法不正确的是（）

A、6位同学成绩的平均数是84 B、6位同学成绩的众数是83 C、6位同学成绩的方差约为7.3 D、6位同学成绩的中位数是81.5

查看试题解析
11. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析
12. 如图，顺次连接四边形ABCD各边中点得四边形EFGH ，要使四边形EFGH为矩形，应添加的条件是（）

A、AB $//$ DC B、AC＝BD C、AC⊥BD D、AB＝DC

查看试题解析

二、填空题

13. 五边形 $A B C D E$ 的内角和是度．

查看试题解析
14. 化简： $(\sqrt{5} + 2) \cdot (\sqrt{5} - 2)$ = ．

查看试题解析
15. 如图，学校有一块长方形草坪，有极少数人为了避开拐角走“捷径”，在草坪内走出了一条“路”，他们仅仅少走了步路（假设2步为1米），却踩伤了花草．

查看试题解析
16. 菱形的一条对角线长为8，其边长是方程x²－8x＋15＝0的一个根，则该菱形的面积为.

查看试题解析
17. 已知关于x的方程 $x^{2} - 3 x + k = 0$ 有两个不相等的实数根，则k的取值范围是．

查看试题解析
18. 如图，矩形ABCD中，AB=3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2} + | - \sqrt{2} | + {(π - 3)}^{0} - \sqrt{4}$ .

查看试题解析
20. 解方程： $x^{2} - 4 = 3 (x - 2)$

查看试题解析
21. 如图所示，在△ABC中，∠ABC＝90°，BD平分∠ABC，DE⊥BC，DF⊥AB.
求证：四边形BEDF是正方形.

查看试题解析
22. 在我市开展的“好书伴我成长”读书活动中，某中学为了解八年级300名学生读书情况，随机调查了八年级50名学生读书的册数.统计数据如下表所示：

册数

0

1

2

3

4

人数

3

13

16

17

1

(1)、50个样本数据的平均数是册、众数是册，中位数是册；

(2)、根据样本数据，估计该校八年级300名学生在本次活动中读书多于2册的人数.

查看试题解析
23. 某中学有一块四边形的空地 $A B C D$ ，如下图所示，学校计划在空地上种植草皮，经测量 $∠ A = 90 °$ ， $A B = 3 m$ ， $B C = 12 m$ ， $C D = 13 m$ ， $D A = 4 m$ ，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
24. 如图，▱ABCD的对角线AC、BD交于点O，E、F是对角线AC上两点，AE＝CF.求证：四边形DEBF是平行四边形.

查看试题解析
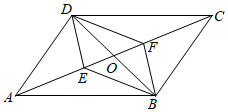25. 新冠病毒肆虐全球，我国的疫情很快得到了控制，并且研发出安全性、有效性均非常高的疫苗，今年七月，国家发布通知，12~17岁未成年人也可接种新冠疫苗.随着全国各地疫苗需求量的急剧增加，经调查发现，北京生物制药厂现有1条生产线最大产能是42万支/天，若每增加1条生产线，每条生产线的最大产能将减少2万支/天，现该厂要保证每天生产疫苗144万支，在既增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
26. 如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．

(1)、求证：▱ABCD是菱形；

(2)、若AB=5，AC=6，求▱ABCD的面积．

查看试题解析

选手	甲	乙	丙	丁
方差（环²）	0.035	0.016	0.022	0.025

册数	0	1	2	3	4
人数	3	13	16	17	1