陕西省西安市莲湖区2022年中考数学模拟试题(三)
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. 的平方根为( )A、 B、 C、 D、2. 下列图形是物理学中的力学、电学等器件的平面示意图,分别代表小车、音叉、凹透镜和砝码,其中是中心对称图形的是( )A、
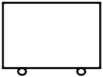 B、
B、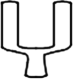 C、
C、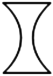 D、
D、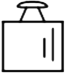 3. 已知 , 则的余角的补角的度数是( )A、 B、 C、 D、4. 如图,在中, , , 分别是斜边上的高和中线,则下列结论不正确的是( )
3. 已知 , 则的余角的补角的度数是( )A、 B、 C、 D、4. 如图,在中, , , 分别是斜边上的高和中线,则下列结论不正确的是( ) A、 B、 C、 D、5. 将一次函数的图象向右平移2个单位后与x轴交于点A,点B的坐标是 , 则线段的长为( )A、5 B、7 C、1 D、6. 如图,在菱形中,对角线与相交于点 , , , 于点 , 延长交于点 , 则的长为( )
A、 B、 C、 D、5. 将一次函数的图象向右平移2个单位后与x轴交于点A,点B的坐标是 , 则线段的长为( )A、5 B、7 C、1 D、6. 如图,在菱形中,对角线与相交于点 , , , 于点 , 延长交于点 , 则的长为( ) A、 B、 C、 D、7. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、8. 已知抛物线经过和两点,则的值为( )A、 B、0 C、1 D、2
A、 B、 C、 D、8. 已知抛物线经过和两点,则的值为( )A、 B、0 C、1 D、2二、填空题
-
9. 计算:.10. 六边形是一个常见的形状,比如古建的窗户、古井的口、佛塔等等.化学上一些分子结构、物理学上的螺母,也采用六边形.正六边形内角和为°.11. 对于任意实数、 , 定义一种运算: , 若 , 则的值为.12. 设 , 为反比例函数图象上两点,若 , , 则k的取值范围是.13. 如图,在等腰中, , , 点在上,点、在上(点在点下方), , 点在内,四边形是平行四边形,连接 , 则面积的最大值为.

三、解答题
-
14. 计算:.15. 解分式方程:.16. 如图,已知 , 射线上一点和直线 , 请利用尺规作图法,在上求作一点 , 使得.(不写作法,保留作图痕迹)

17. 解不等式组: , 并将解集在数轴上表示出来. 18. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何(马、牛单价各是多少两)?”19. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.
18. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何(马、牛单价各是多少两)?”19. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.
注:如果选择多个条件分别解答,按第一个解答计分.
 20. 陕西考古博物馆是集科研、公众教育和社会服务为一体的,重点展示考古工作和考古学科发展的全国乃至全世界专题性博物馆.周末,爸爸带着晓玲和姐姐重点参观了考古发现篇章,考古发现篇又分为:一、“探源文明,构建先史”;二、“寻踪帝国,盛世再现”;三、“追迹古都,陶冶风雅”三个单元,参观结束后回到家,晓玲和姐姐各自从这三个单元中随机选择一个为主题写一篇小作文.(1)、晓玲选择“探源文明,构建先史”为主题,这一事件是事件;(填“随机”,“不可能”或“必然”)(2)、请用画树状图或列表法,求晓玲和姐姐选择同一个单元为主题的概率.21. 某校数学社团开展“探索生活中的数学”研学活动,准备测量秦始皇雕塑的高度.如图所示,首先,在阳光下,某一时刻,小玉在雕塑影子顶端处竖立一根高2米的标杆 , 此时测得标杆的影子为2米;然后,在处竖立一根高2.5米的标杆 , 小婷从处沿后退0.8米到处恰好看到点、在一条直线上,小婷的眼睛到地面的距离米,米,已知 , , , , 点、、、、在同一水平直线上,请根据以上数据求出秦始皇雕塑的高度.
20. 陕西考古博物馆是集科研、公众教育和社会服务为一体的,重点展示考古工作和考古学科发展的全国乃至全世界专题性博物馆.周末,爸爸带着晓玲和姐姐重点参观了考古发现篇章,考古发现篇又分为:一、“探源文明,构建先史”;二、“寻踪帝国,盛世再现”;三、“追迹古都,陶冶风雅”三个单元,参观结束后回到家,晓玲和姐姐各自从这三个单元中随机选择一个为主题写一篇小作文.(1)、晓玲选择“探源文明,构建先史”为主题,这一事件是事件;(填“随机”,“不可能”或“必然”)(2)、请用画树状图或列表法,求晓玲和姐姐选择同一个单元为主题的概率.21. 某校数学社团开展“探索生活中的数学”研学活动,准备测量秦始皇雕塑的高度.如图所示,首先,在阳光下,某一时刻,小玉在雕塑影子顶端处竖立一根高2米的标杆 , 此时测得标杆的影子为2米;然后,在处竖立一根高2.5米的标杆 , 小婷从处沿后退0.8米到处恰好看到点、在一条直线上,小婷的眼睛到地面的距离米,米,已知 , , , , 点、、、、在同一水平直线上,请根据以上数据求出秦始皇雕塑的高度.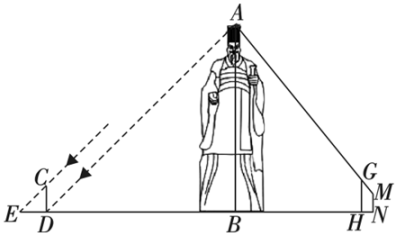 22. 4月16日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,中国“太空出差三人组”成员平安回到了祖国大地.星空浩瀚无限,探索永无止境,我们都是“追梦人”,为了庆祝我国航天事业的发展,某校举行航空航天作品展,为了解学生上交作品情况,随机调查了部分学生上交作品件数,根据调查结果,绘制了如下两幅不完整的统计图.
22. 4月16日,神舟十三号载人飞船返回舱在东风着陆场成功着陆,中国“太空出差三人组”成员平安回到了祖国大地.星空浩瀚无限,探索永无止境,我们都是“追梦人”,为了庆祝我国航天事业的发展,某校举行航空航天作品展,为了解学生上交作品情况,随机调查了部分学生上交作品件数,根据调查结果,绘制了如下两幅不完整的统计图.
请根据相关信息,解答下列问题:
(1)、补全两幅统计图;(2)、求所抽取学生上交作品件数的众数与中位数;(3)、求所抽取学生上交作品件数的平均数,若该校共有1200名学生,请估计上交的作品一共有多少件?23. 将生态资源转化为经济资源,促进产业融合,生态绿色振兴之路是关键.为做好生态与产业融合,推进农业农村绿色发展,某生态示范园培育出品种优良的甲种有机水果,该有机水果同城销售方法是:送货上门,除每次收取送货费10元外,购买水果不超过时按每千克20元收费,超过时,超出部分按每千克15元收费.设同城顾客购买甲种有机水果,所需总费用为(元).(1)、求与之间的函数关系式;(2)、已知同城李阿姨在该生态示范园一次订购甲种有机水果共花费155元,求李阿姨这次订购甲种有机水果多少千克?24. 如图,内接于 , 是的直径,点是上一点,连接、 , 过点作 , 交的延长线于点 , 平分. (1)、求证:是的切线;(2)、若 , 的半径为6,求的长.25. 如图,已知直线与轴交于点A,与轴交于点 , 抛物线经过点A,与轴的另一个交点为 , 交轴于点.
(1)、求证:是的切线;(2)、若 , 的半径为6,求的长.25. 如图,已知直线与轴交于点A,与轴交于点 , 抛物线经过点A,与轴的另一个交点为 , 交轴于点. (1)、求抛物线的函数表达式及点的坐标;(2)、点是轴上的点,在轴右侧的抛物线上是否存在点 , 使得与相似,且点与点为对应点,若存在,请求出点的坐标,若不存在,请说明理由.26.
(1)、求抛物线的函数表达式及点的坐标;(2)、点是轴上的点,在轴右侧的抛物线上是否存在点 , 使得与相似,且点与点为对应点,若存在,请求出点的坐标,若不存在,请说明理由.26.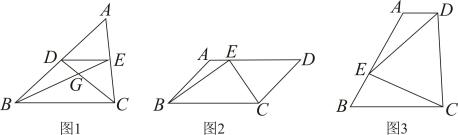 (1)、问题提出:如图1,在中,点、分别是、的中点,连接、、 , 与交于点 , 若 , 则;(2)、问题探究:如图2,在中, , , 点是上一点(可与端点重合),连接、 , , 求面积的最小值;(3)、问题解决:某湿地公园拟建一个梯形花园 , 示意图如图3所示,其中 , , .管理员计划在区域种植水生植物,在区域种植甲种花卉.根据设计要求,要满足点在上, , 是锐角,且 , 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?
(1)、问题提出:如图1,在中,点、分别是、的中点,连接、、 , 与交于点 , 若 , 则;(2)、问题探究:如图2,在中, , , 点是上一点(可与端点重合),连接、 , , 求面积的最小值;(3)、问题解决:某湿地公园拟建一个梯形花园 , 示意图如图3所示,其中 , , .管理员计划在区域种植水生植物,在区域种植甲种花卉.根据设计要求,要满足点在上, , 是锐角,且 , 若种植水生植物每平方米需400元,种植甲种花卉每平方米需100元,求种植水生植物和种植甲种花卉所需总费用至少为多少元?