江苏省宿迁市泗洪县2022年中考三模数学试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. 下列各数中最大的是( )A、 B、 C、0 D、12. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
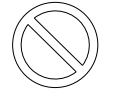 B、
B、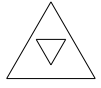 C、
C、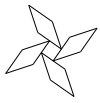 D、
D、 3. 某市四月份连续7天的最高气温依次是:18,15,16,15,16,18,19单位(℃),则这组数据的中位数是( )A、16℃ B、17℃ C、18℃ D、19℃4. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( )
3. 某市四月份连续7天的最高气温依次是:18,15,16,15,16,18,19单位(℃),则这组数据的中位数是( )A、16℃ B、17℃ C、18℃ D、19℃4. 如图是由4个相同的小正方体构成的一个组合体,该组合体的三视图中完全相同的是( ) A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同5. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、26. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三个视图均相同5. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、26. 已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )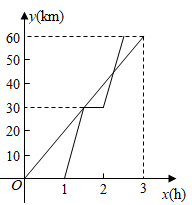 A、15km B、16km C、44km D、45km7. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、15km B、16km C、44km D、45km7. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、58. 已知抛物线的对称轴在轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则的值是( )A、或2 B、 C、2 D、
A、2 B、3 C、4 D、58. 已知抛物线的对称轴在轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则的值是( )A、或2 B、 C、2 D、二、填空题
-
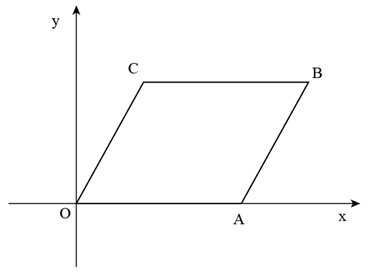
9. 因式分解 = .10. 函数y= 中,自变量x的取值范围是 .11. 正多边形的一个外角等于 , 这个多边形的边数是.12. 化简:.13. 圆锥的高是 , 母线长是 , 则这个圆锥的侧面积为.(结果保留)14. 关于的方程的两根分别为、 , 则的值为.15. 如图,在平面直角坐标系 中,四边形 是平行四边形,其中点A在x轴正半轴上.若 ,则点A的坐标是.
 16. 如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为.
16. 如图,从一个大正方形中截去面积为和的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为.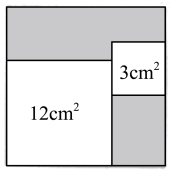 17. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为.
17. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为. 18. 如图①,在中, , , 点E是边AB的中点,点P是边BC上一动点,设 , .图②是y关于x的函数图象,其中H是图象上的最低点.那么的值为.
18. 如图①,在中, , , 点E是边AB的中点,点P是边BC上一动点,设 , .图②是y关于x的函数图象,其中H是图象上的最低点.那么的值为.

三、解答题
-
19. 计算:.20. 解不等式组:21. 教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求,初中生每天睡眠时间应达到.某初中学校综合实践小组为了解该校学生每天的睡眠时间,随机调查了部分学生,将学生睡眠时间分为 , , , 四组(每名学生必须选择且只能选择其中的一种情况):组:睡眠时间 , 组:睡眠时间 , 组:睡眠时间 , 组:睡眠时间.
如图1和图2是根据调查结果绘制的不完整的统计图,请根据图中提供的信息,解答下列问题:
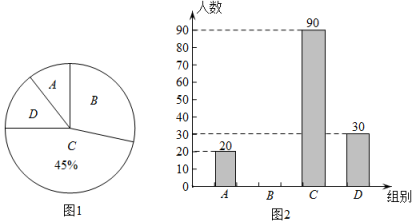 (1)、被调查的学生有人,扇形统计图中组对应的扇形圆心角的度数°;(2)、通过计算补全条形统计图;(3)、请估计全校2000名学生中睡眠时间不足的人数.22. 如图,在中, , , 通过尺规作图,得到直线和射线 , 仔细观察作图痕迹,完成下列问题:
(1)、被调查的学生有人,扇形统计图中组对应的扇形圆心角的度数°;(2)、通过计算补全条形统计图;(3)、请估计全校2000名学生中睡眠时间不足的人数.22. 如图,在中, , , 通过尺规作图,得到直线和射线 , 仔细观察作图痕迹,完成下列问题: (1)、直线是线段的线,射线是的线;(2)、求的度数.23. 如图,一次函数的图象与轴、轴分别交于 , , 与反比例函数的图象交于点 , .
(1)、直线是线段的线,射线是的线;(2)、求的度数.23. 如图,一次函数的图象与轴、轴分别交于 , , 与反比例函数的图象交于点 , .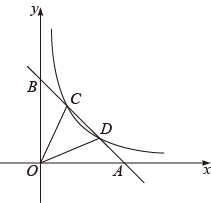 (1)、分别求出两个函数的表达式;(2)、连接 , , 求的面积.24. 如图所示,玫瑰家园小区有甲、乙两栋居民楼,小明在甲居民楼的楼顶处观测乙居民楼楼底处的俯角是 , 观测乙居民楼楼顶处的仰角为 , 已知甲居民楼的高为 , 求乙居民楼的高.(参考数据: , , 结果精确到)
(1)、分别求出两个函数的表达式;(2)、连接 , , 求的面积.24. 如图所示,玫瑰家园小区有甲、乙两栋居民楼,小明在甲居民楼的楼顶处观测乙居民楼楼底处的俯角是 , 观测乙居民楼楼顶处的仰角为 , 已知甲居民楼的高为 , 求乙居民楼的高.(参考数据: , , 结果精确到) 25. 4张相同的卡片上分别写有数字0、1、 、3,将卡片的背面朝上,洗匀后从中任意抽取1张.将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是负数的概率为;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜:否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用画树状图或列表等方法说明理由).26. 2022年5月8日是“母亲节”,小明买了一束百合和康乃馨组合的鲜花送给妈妈,以表祝福.在买花过程中,爱思考的小明发现一个数学问题:3支康乃馨的价格比2支百合的价格多2元,买2支百合和1支康乃馨共花费14元.如果买一束百合和康乃馨组合的鲜花共11支,且百合不少于2支,那么怎样组合,能使费用支出最少?请你帮助小明解决这个数学问题.27. 定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为圆美四边形.
25. 4张相同的卡片上分别写有数字0、1、 、3,将卡片的背面朝上,洗匀后从中任意抽取1张.将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.(1)、第一次抽取的卡片上数字是负数的概率为;(2)、小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜:否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用画树状图或列表等方法说明理由).26. 2022年5月8日是“母亲节”,小明买了一束百合和康乃馨组合的鲜花送给妈妈,以表祝福.在买花过程中,爱思考的小明发现一个数学问题:3支康乃馨的价格比2支百合的价格多2元,买2支百合和1支康乃馨共花费14元.如果买一束百合和康乃馨组合的鲜花共11支,且百合不少于2支,那么怎样组合,能使费用支出最少?请你帮助小明解决这个数学问题.27. 定义:若一个圆内接四边形的两条对角线互相垂直,则称这个四边形为圆美四边形. (1)、选择:下列四边形中,一定是圆美四边形的是( )A、平行四边形 B、矩形 C、菱形 D、正方形(2)、如图1,在等腰中, , , 经过点的交边于点 , 交于点 , 连接 , 若四边形为圆美四边形,求的长;(3)、如图2,是外接圆的直径,交于点 , 点在上,延长交于点 , 已知.问四边形是圆美四边形吗?为什么?28. 如图,直线与抛物线相交于点和点 , 抛物线与轴的交点分别为、(点在点的左侧),点在线段上运动(不与点A、重合),过点作直线轴于点 , 交抛物线于点.
(1)、选择:下列四边形中,一定是圆美四边形的是( )A、平行四边形 B、矩形 C、菱形 D、正方形(2)、如图1,在等腰中, , , 经过点的交边于点 , 交于点 , 连接 , 若四边形为圆美四边形,求的长;(3)、如图2,是外接圆的直径,交于点 , 点在上,延长交于点 , 已知.问四边形是圆美四边形吗?为什么?28. 如图,直线与抛物线相交于点和点 , 抛物线与轴的交点分别为、(点在点的左侧),点在线段上运动(不与点A、重合),过点作直线轴于点 , 交抛物线于点. (1)、求抛物线的函数表达式;(2)、如图1,连接 , 是否存在点 , 使是直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,过点作于点 , 当的周长最大时,求点坐标,并求出此时的面积.
(1)、求抛物线的函数表达式;(2)、如图1,连接 , 是否存在点 , 使是直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,过点作于点 , 当的周长最大时,求点坐标,并求出此时的面积.