江苏省沭阳县2022年九年级下学期中考调研数学试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. -2022的相反数是( )A、-2022 B、2022 C、 D、2. 截至2022年3月24日,“祝融号”火星车在距离地球277000000千米的火星表面工作306个火星日,数据277000000用科学记数法可表示为( )A、277×106 B、27.7×107 C、2.77×108 D、0.277×1093. 下列计算正确的是( )A、 B、 C、 D、4. 下列生活现象,可以用基本事实“两点之间,线段最短”解释的是( )A、汽车的雨刮器把玻璃上的水刷干净 B、开山挖隧道,把上坡下坡的盘山公路改为平直的隧道 C、公园的喷泉中,喷水龙头喷出的圆形水面 D、建筑工人通过在两个柱子之间拉一条绳子砌墙5. 已知 , 则锐角A的度数是( )
A、 B、 C、 D、6. 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )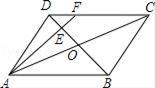 A、1:3 B、1:4 C、2:3 D、1:27. 已知长方形纸条ABCD,点E、G在AD边上,点F、H在BC边上.将纸条分别沿着EF、GH折叠,如图,当DC恰好落在上时,与的数量关系是( )
A、1:3 B、1:4 C、2:3 D、1:27. 已知长方形纸条ABCD,点E、G在AD边上,点F、H在BC边上.将纸条分别沿着EF、GH折叠,如图,当DC恰好落在上时,与的数量关系是( ) A、 B、 C、 D、8. 如图,位于第一象限, , 直角顶点A在直线上,其中点A的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若函数的图象与有交点,则k的最大值是( )
A、 B、 C、 D、8. 如图,位于第一象限, , 直角顶点A在直线上,其中点A的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若函数的图象与有交点,则k的最大值是( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
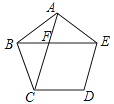
9. 分解因式: .10. 已知: , 则.11. 若不等式 , 两边同除以m,得 , 则m的取值范围为.12. 圆锥的底面半径为3,展开图是圆心角的扇形,则这个圆锥的侧面积是.13. 甲、乙两位同学在近五次数学测试中,平均成绩均为85分,方差分别为 , 甲、乙两位同学成绩较稳定的是同学.14. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .
 15. 二次函数的部分图象如图所示,对称轴为直线 , 当时,x的取值范围是.
15. 二次函数的部分图象如图所示,对称轴为直线 , 当时,x的取值范围是. 16. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取).
16. 如图,是一个小型花园,阴影部分为一个圆形水池,且与三边相切,已知 , , , 若从天空飘落下一片树叶恰好落入花园里,则落入水池的概率(取). 17. 如图,在平面直角坐标系中,一次函数 的图象分别交 、 轴于点 、 ,将直线 绕点 按顺时针方向旋转 ,交 轴于点 ,则直线 的函数表达式是.
17. 如图,在平面直角坐标系中,一次函数 的图象分别交 、 轴于点 、 ,将直线 绕点 按顺时针方向旋转 ,交 轴于点 ,则直线 的函数表达式是. 18. 如图,已知A点从点出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t秒后,以O,A为顶点作菱形 , 使B,C点都在第一象限内,且 , 若以为圆心,为半径的圆恰好与所在的直线相切,则.
18. 如图,已知A点从点出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t秒后,以O,A为顶点作菱形 , 使B,C点都在第一象限内,且 , 若以为圆心,为半径的圆恰好与所在的直线相切,则.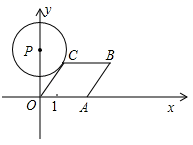
三、解答题
-
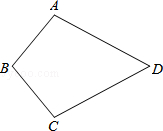
19. 计算与解方程:(1)、(2)、20. 先化简:( ﹣a+1)÷ ,并从0,﹣1,2中选一个合适的数作为a的值代入求值.21. 如图,已知:AB=CB,AD=CD,求证:∠A=∠C.
 22. 某校开展社团活动,项目有:羽毛球、葫芦丝、茶艺表演.小红从三项中随机抽取,求下列事件的概率.(1)、抽取一项,恰好是羽毛球的概率是;(2)、抽取两项,请用列表法或画树状图,求出羽毛球被抽中的概率.23. 某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
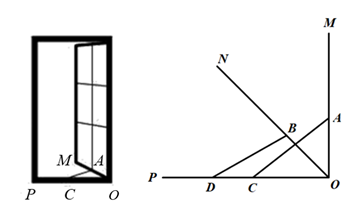
22. 某校开展社团活动,项目有:羽毛球、葫芦丝、茶艺表演.小红从三项中随机抽取,求下列事件的概率.(1)、抽取一项,恰好是羽毛球的概率是;(2)、抽取两项,请用列表法或画树状图,求出羽毛球被抽中的概率.23. 某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: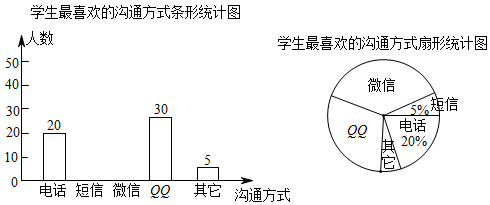 (1)、这次统计共抽查了名学生;(2)、将条形统计图补充完整;(3)、该校共有2000名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?24. 如图,一扇窗户垂直打开,即打开到的状态,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转到达ON位置,此时,点A、C的对应位置分别是点B、D.测出此时为 , BO的长为.求滑动支架AC的长.
(1)、这次统计共抽查了名学生;(2)、将条形统计图补充完整;(3)、该校共有2000名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?24. 如图,一扇窗户垂直打开,即打开到的状态,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转到达ON位置,此时,点A、C的对应位置分别是点B、D.测出此时为 , BO的长为.求滑动支架AC的长.(精确到).
 25. 如图,△ABC内接于⊙O,AB是⊙O的直径,AD是⊙O的切线,点A为切点,AD=AC,连接DC交AB于点E.
25. 如图,△ABC内接于⊙O,AB是⊙O的直径,AD是⊙O的切线,点A为切点,AD=AC,连接DC交AB于点E. (1)、求证,.(2)、若 , , 求BC的长.26. 2022年,冬奥会和冬残奥会在北京举办,冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.2021年11月初,奥林匹克官方旗舰店上架了“冰墩域”和“雪容融”这两款毛绒玩具,当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为33000元;12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为54000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩境”和“雪容融”的成本分别为90元/个和60元/个;旗舰店准备用60000元全部购进这两款毛绒玩具.该旗舰店进货时,厂家要求“雪容融”的购进数量不超过“冰墩墩”的购进数量,若购进的这两款毛绒玩具全部售出,则如何设计进货方案才能使该旗舰店当月销售利润最大,并求出最大利润.27. 如图1,在矩形ABCD中,E、F、G分别为边BC、AB、AD的中点,连接DF、EF,H为DF中点,连接GH,将绕点B旋转.
(1)、求证,.(2)、若 , , 求BC的长.26. 2022年,冬奥会和冬残奥会在北京举办,冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”深受广大人民的喜爱.2021年11月初,奥林匹克官方旗舰店上架了“冰墩域”和“雪容融”这两款毛绒玩具,当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为33000元;12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为54000元.(1)、求“冰墩墩”和“雪容融”的销售单价;(2)、已知“冰墩境”和“雪容融”的成本分别为90元/个和60元/个;旗舰店准备用60000元全部购进这两款毛绒玩具.该旗舰店进货时,厂家要求“雪容融”的购进数量不超过“冰墩墩”的购进数量,若购进的这两款毛绒玩具全部售出,则如何设计进货方案才能使该旗舰店当月销售利润最大,并求出最大利润.27. 如图1,在矩形ABCD中,E、F、G分别为边BC、AB、AD的中点,连接DF、EF,H为DF中点,连接GH,将绕点B旋转. (1)、当旋转到如图2的位置,连接AF、CE,若 , 且 , 则 , ;(2)、已知.
(1)、当旋转到如图2的位置,连接AF、CE,若 , 且 , 则 , ;(2)、已知.①当旋转到如图3位置时,连接CE,猜想GH与CE之间的数量关系和位置关系,并说明理由.
②在旋转过程中,射线GH,CE相交于点Q,连接AQ,AQ有最小值吗?若有,请直接写出AQ的最小值;若没有,请说明理由.
28. 如图1,在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C. (1)、求点A的坐标;(2)、如图2,连接AC,点D为线段AC下方抛物线上一动点,过点D作轴交线段AC于E点,连接EO、AD,记的面积为 , 的面积为 , 求的最大值及此时点D的坐标;(3)、如图3,连接CB,并将抛物线沿射线CB方向平移个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线与y轴的交点,当为以AM为腰的等腰三角形时,请直接写出点N的坐标.
(1)、求点A的坐标;(2)、如图2,连接AC,点D为线段AC下方抛物线上一动点,过点D作轴交线段AC于E点,连接EO、AD,记的面积为 , 的面积为 , 求的最大值及此时点D的坐标;(3)、如图3,连接CB,并将抛物线沿射线CB方向平移个单位长度得到新抛物线,动点N在原抛物线的对称轴上,点M为新抛物线与y轴的交点,当为以AM为腰的等腰三角形时,请直接写出点N的坐标.