湖北省黄冈市2022年九年级三模考试数学试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列事物所运用的原理不属于三角形稳定性的是( )A、长方形门框的斜拉条 B、埃及金字塔 C、三角形房架 D、学校的电动伸缩大门3. 如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
 A、35° B、40° C、45° D、50°4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、且 D、且6. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A、35° B、40° C、45° D、50°4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、且 D、且6. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )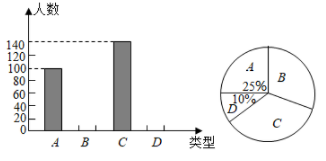 A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人7. 如图是小明做的一个风筝支架示意图,已知 , , , 则的长是( ).
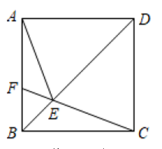
A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人7. 如图是小明做的一个风筝支架示意图,已知 , , , 则的长是( ). A、 B、 C、 D、8. 如图,在矩形中, , , 是对角线的交点,过作于点 , 的延长线与的平分线相交于点 , 与交于点.给出下列四个结论:①;②;③;④.其中正确结论有( ).
A、 B、 C、 D、8. 如图,在矩形中, , , 是对角线的交点,过作于点 , 的延长线与的平分线相交于点 , 与交于点.给出下列四个结论:①;②;③;④.其中正确结论有( ). A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 式子 中x的取值范围是.10. 不等式-3x-1≥-10的正整数解为11. 如图,在ABC中,点D、E分别在AB、BC上,AFBC,且∠1=∠2,如果∠B=30°,且∠2=70°,那么∠BAC=.
 12. 已知a,b是方程x2+3x﹣5=0的两个实数根,则a2﹣3b+2020的值是.13. 小张、小王和小李三人相约去参加“抗疫情党员志愿者进社区服务”活动,现在有A、B、C三个社区可供随机选择,他们三人恰好进入同一社区的概率是.14. 如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为.
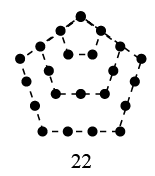
12. 已知a,b是方程x2+3x﹣5=0的两个实数根,则a2﹣3b+2020的值是.13. 小张、小王和小李三人相约去参加“抗疫情党员志愿者进社区服务”活动,现在有A、B、C三个社区可供随机选择,他们三人恰好进入同一社区的概率是.14. 如图①,“东方之门”通过简单的几何曲线处理,将传统文化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图②,“门”的内侧曲线呈抛物线形,已知其底部宽度为80米,高度为200米.则离地面150米处的水平宽度(即CD的长)为. 15. 两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作 , 第2个五角形数记作 , 第3个五角形数记作 , 第4个五角形数记作 , …,若按此规律继续下去,则.
15. 两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作 , 第2个五角形数记作 , 第3个五角形数记作 , 第4个五角形数记作 , …,若按此规律继续下去,则.


 16. 如图,正方形中,点、从点出发,以的速度分别沿和的路径匀速运动,同时到达点时停止运动.连接 , 设的长为 , 运动时间为 , 则与(秒)的函数图象如图所示.当秒时,的长是.
16. 如图,正方形中,点、从点出发,以的速度分别沿和的路径匀速运动,同时到达点时停止运动.连接 , 设的长为 , 运动时间为 , 则与(秒)的函数图象如图所示.当秒时,的长是.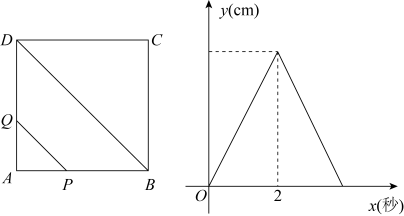
三、解答题
-
17. 已知a+b= , ab=﹣ , 先因式分解,再求值:a3b+2a2b2+ab3.18. 如图,不透明的管中放置着三根完全相同的绳子AA1、BB1、CC1.在不看的情况下,小明从左端A、B、C三个绳头中随机选一个绳头,小刚从右端A1、B1、C1三个绳头中随机选一个绳头,用画树状图(或列表)的方法,求小明和小刚选中的两个绳头恰好是同一根绳子的概率.
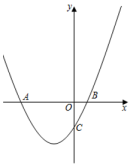
 19. 学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.(1)、购买一件A道具和一件B道具各需要多少元?(2)、根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.求道具A最多购买多少件?20. 如图,一次函数的图象与反比例函数的图象交于A,B两点,过点A做x轴的垂线,垂足为M,面积为1.
19. 学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.(1)、购买一件A道具和一件B道具各需要多少元?(2)、根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.求道具A最多购买多少件?20. 如图,一次函数的图象与反比例函数的图象交于A,B两点,过点A做x轴的垂线,垂足为M,面积为1.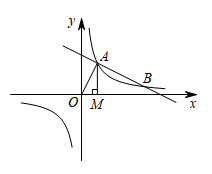 (1)、求反比例函数的解析式;(2)、在x轴上求一点P,使的值最大,并求出其最大值和P点坐标.21. 如图,的直径 , 点为上一点,为的切线,于点 , 分别交 , 于 , 两点.
(1)、求反比例函数的解析式;(2)、在x轴上求一点P,使的值最大,并求出其最大值和P点坐标.21. 如图,的直径 , 点为上一点,为的切线,于点 , 分别交 , 于 , 两点. (1)、求证:;(2)、若 , 求图中两处(点左侧与点右侧)阴影部分的面积之和.22. 小亮创办了一个微店商铺,营销一款小型LED护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量p(盏)与时间x(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏.护眼台灯的销售价格y(元/盏)与时间x(天)之间符合函数关系式( , 且x为整数).(1)、求日销售量p(盏)与时间x(天)之间的函数关系式;(2)、在这20天中,哪天的日销售利润最大?最大日销售利润是多少?(3)、“双十一”当天,小亮采用如下促销方式:销售价格比前20天中最高日销售价格降低a元;日销售量比前20天最高日销售量提高了7a盏;日销售利润比前20天中的最大日销售利润多了30元,求a的值.(注:销售利润=售价-成本).
(1)、求证:;(2)、若 , 求图中两处(点左侧与点右侧)阴影部分的面积之和.22. 小亮创办了一个微店商铺,营销一款小型LED护眼台灯,成本是20元/盏,在“双十一”前20天进行了网上销售后发现,该台灯的日销售量p(盏)与时间x(天)之间满足一次函数关系,且第1天销售了78盏,第2天销售了76盏.护眼台灯的销售价格y(元/盏)与时间x(天)之间符合函数关系式( , 且x为整数).(1)、求日销售量p(盏)与时间x(天)之间的函数关系式;(2)、在这20天中,哪天的日销售利润最大?最大日销售利润是多少?(3)、“双十一”当天,小亮采用如下促销方式:销售价格比前20天中最高日销售价格降低a元;日销售量比前20天最高日销售量提高了7a盏;日销售利润比前20天中的最大日销售利润多了30元,求a的值.(注:销售利润=售价-成本).