贵州省铜仁市2022年中考数学复习备考第三次模拟试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. 在-2022,2,0,4四个数中,其中最小的数是( )A、 B、2. C、0 D、42. 下列图案可以通过一个“基本图形”平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用四舍五入法求0.0000300449的近似值,并保留三个有效数字,结果用科学记数法表示正确的是( ).A、 B、 C、 D、4. 为全面落实双减工作,扎实开展课后服务,某学校在开展篮球社团活动中,其中某小组篮球队13名队员的年龄情况如下,则这个队队员年龄的众数和中位数为( )
3. 用四舍五入法求0.0000300449的近似值,并保留三个有效数字,结果用科学记数法表示正确的是( ).A、 B、 C、 D、4. 为全面落实双减工作,扎实开展课后服务,某学校在开展篮球社团活动中,其中某小组篮球队13名队员的年龄情况如下,则这个队队员年龄的众数和中位数为( )年龄(岁)
14
15
16
17
18
人数(人)
1
4
3
3
2
A、15,15 B、15,15.5 C、15,16 D、16,155. 分式可变形为( )A、 B、 C、 D、6. 实数a,b在数轴上的位置如图所示,化简的结果是( ). A、 B、 C、 D、7. △ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )
A、 B、 C、 D、7. △ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )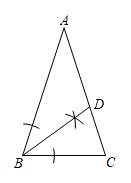 A、AD=BD B、∠BDC=72° C、S△ABD:S△BCD=BC:AC D、△BCD的周长=AB+BC8. 如图,正五边形ABCDE边长为6,以A为圆心,AB为半径画圆,图中阴影部分的面积为( ).
A、AD=BD B、∠BDC=72° C、S△ABD:S△BCD=BC:AC D、△BCD的周长=AB+BC8. 如图,正五边形ABCDE边长为6,以A为圆心,AB为半径画圆,图中阴影部分的面积为( ).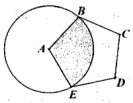 A、 B、 C、 D、9. 已知,如图长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕为EF,则BEF的面积为( )
A、 B、 C、 D、9. 已知,如图长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕为EF,则BEF的面积为( ) A、6 B、7.5 C、12 D、1510. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,有下列4个结论:①abc>0;②a+c>b;③4a+2b+c>0;④a+b≥am2+bm(m是任意实数).其中正确结论的个数是( )
A、6 B、7.5 C、12 D、1510. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,有下列4个结论:①abc>0;②a+c>b;③4a+2b+c>0;④a+b≥am2+bm(m是任意实数).其中正确结论的个数是( )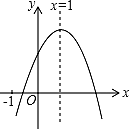 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,是一个简单的数值运算程序.当输入x的值为 , 则输出的数值为.12. 若是某个二元一次方程的一个解,则该方程可能是 (请写出满足条件的一个答案即可)13. 一个三角形的三边长均为整数.已知其中两边长为3和5,第三边长是不等式组的正整数解.则第三边的长为:.14.
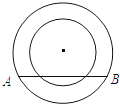
如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .
 15. 如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中 , , ,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是 .
15. 如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中 , , ,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是 .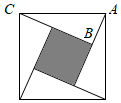 16. 如图,菱形的边长为 , 且 , E是中点,P点在上,则的最小值为.
16. 如图,菱形的边长为 , 且 , E是中点,P点在上,则的最小值为.
三、解答题
-
17. 18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.
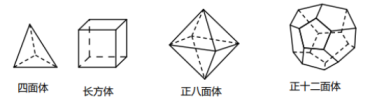 (1)、根据上面的多面体模型,直接写出表格中的m,n的值,则 , .
(1)、根据上面的多面体模型,直接写出表格中的m,n的值,则 , .多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
m
6
12
正八面体
n
8
12
正十二面体
20
12
30
(2)、你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(3)、一个多面体的面数等于顶点数,且这个多面体有30条棱,求这个多面体的面数.18. 小明想用镜子测量校园内一棵松树的高度,如图所示,他把镜子放在水平地面上的C点,沿着直线 后退到点F,这时恰好在镜子里看到树稍顶点A的像,量得 米, 米.已知 、 均与地面 垂直,小明的眼睛距离地面1.5米(即 米),请你求出松树 的高. 19. 为了培养学生成为具有“社会责任、学术素养、创新能力、国际视野”的未来人才,我校提出“让每一个孩子成长为一棵参天大树”的“树”课程理念,数学科开发了四门“树”课程供学生选择:A.趣味数学;B.棋海巡航;C.中外数学史;D.数独与幻方.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
19. 为了培养学生成为具有“社会责任、学术素养、创新能力、国际视野”的未来人才,我校提出“让每一个孩子成长为一棵参天大树”的“树”课程理念,数学科开发了四门“树”课程供学生选择:A.趣味数学;B.棋海巡航;C.中外数学史;D.数独与幻方.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图. (1)、该年级学生小李随机选取了一门课程,则小李选中课程C的概率是 ;(2)、根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数是;(3)、该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C.那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.20. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )
(1)、该年级学生小李随机选取了一门课程,则小李选中课程C的概率是 ;(2)、根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数是;(3)、该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C.那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.20. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )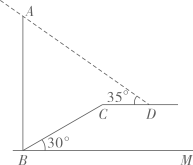
 21. 国庆假期一部《长津湖》带给我们极大的震撼,面对美军的先进武器,志愿军不怕牺牲,以一敌百,更是有很多技术精湛的“神投手”.某志愿军身负重伤,不轻易放弃,用最后一丝力气投出一枚手榴弹,如果把该志愿军投出的手榴弹轨迹作为一抛物线,如图所示,手榴弹飞行的最大高度为10米,此时水平飞行距离为9米,手榴弹离手点离地面高度为1.9米.
21. 国庆假期一部《长津湖》带给我们极大的震撼,面对美军的先进武器,志愿军不怕牺牲,以一敌百,更是有很多技术精湛的“神投手”.某志愿军身负重伤,不轻易放弃,用最后一丝力气投出一枚手榴弹,如果把该志愿军投出的手榴弹轨迹作为一抛物线,如图所示,手榴弹飞行的最大高度为10米,此时水平飞行距离为9米,手榴弹离手点离地面高度为1.9米. (1)、求此抛物线解析式;(2)、求志愿军同志的手榴弹扔了多远?22. 某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.(1)、求购买一个甲奖品和一个乙奖品各需多少元?(2)、经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?23. 如图,点在以为直径的上,平分交于点 , 过作的垂线,垂足为.
(1)、求此抛物线解析式;(2)、求志愿军同志的手榴弹扔了多远?22. 某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.(1)、求购买一个甲奖品和一个乙奖品各需多少元?(2)、经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?23. 如图,点在以为直径的上,平分交于点 , 过作的垂线,垂足为. (1)、求证:与相切;(2)、请用线段、表示的长,并说明理由.24.(1)、探索发现:如图1,已知中, , , 直线l过点C,过点A作 , 过点B作 , 垂足分别为D、E.求证:.
(1)、求证:与相切;(2)、请用线段、表示的长,并说明理由.24.(1)、探索发现:如图1,已知中, , , 直线l过点C,过点A作 , 过点B作 , 垂足分别为D、E.求证:. (2)、迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为 , 求点M的坐标.
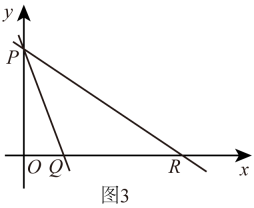
(2)、迁移应用:如图2,将一块等腰直角的三角板放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点N的坐标为 , 求点M的坐标. (3)、拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.
(3)、拓展应用:如图3,在平面直角坐标系内,已知直线与y轴交于点P,与x轴交于点Q,将直线绕P点沿逆时针方向旋转后,所得的直线交x轴于点R.求点R的坐标.