广西梧州市重点中学2022年中考数学模拟诊断试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. 若与2互为相反数,则的值是( )A、-2 B、0 C、2 D、42. 下列图形中不是轴对称图形的是( )A、等边三角形 B、正方形 C、平行四边形 D、正五边形3. 已知一粒米的质量是0.000021千克,这个数字用科学记数法表示( )A、 千克 B、 千克 C、 千克 D、 千克4. 下列展开图中,不是正方体展开图的是( )A、
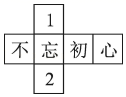 B、
B、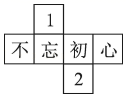 C、
C、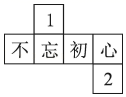 D、
D、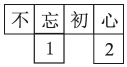 5. 团支部王书记将6本莫言作品分别放在6个完全相同的不透明礼盒中,准备将它们奖给小李等6位在读书活动中表现突出的员工.这些奖品中3本是《红高粱家庭》,2本是《蛙》,1本是《生死疲劳》.小李从中随机取一个礼盒,恰好取到《蛙》的概率是A、 B、 C、 D、6. 不等式的解集在数轴上表示正确的是( )A、
5. 团支部王书记将6本莫言作品分别放在6个完全相同的不透明礼盒中,准备将它们奖给小李等6位在读书活动中表现突出的员工.这些奖品中3本是《红高粱家庭》,2本是《蛙》,1本是《生死疲劳》.小李从中随机取一个礼盒,恰好取到《蛙》的概率是A、 B、 C、 D、6. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、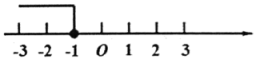 7. 如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )
7. 如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF等于( )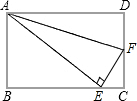 A、 B、1 C、 D、28. 一个正多边形的每个外角都等于40°,则它的内角和是( )A、 B、 C、 D、9. 下列运算正确的是( )A、 B、 C、 D、10. 将长方形纸片沿AC折叠后点B落在点E处,则线段BE与AC的关系是( )
A、 B、1 C、 D、28. 一个正多边形的每个外角都等于40°,则它的内角和是( )A、 B、 C、 D、9. 下列运算正确的是( )A、 B、 C、 D、10. 将长方形纸片沿AC折叠后点B落在点E处,则线段BE与AC的关系是( )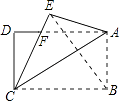 A、AC=BE B、AC⊥BE C、AC⊥BE且AC=BE D、AC⊥BE且AC平分BE11. 如图,以O为圆心,半径为2的圆与反比例函数y=(x>0)的图象交于A、B两点,则的长度为( )
A、AC=BE B、AC⊥BE C、AC⊥BE且AC=BE D、AC⊥BE且AC平分BE11. 如图,以O为圆心,半径为2的圆与反比例函数y=(x>0)的图象交于A、B两点,则的长度为( ) A、 B、 C、 D、12. 如图,等腰直角三角形ABC的直角顶点C与坐标原点重合,分别过点A、B作x轴的垂线,垂足为D、E,点A的坐标为(-2,5),则线段DE的长为( )
A、 B、 C、 D、12. 如图,等腰直角三角形ABC的直角顶点C与坐标原点重合,分别过点A、B作x轴的垂线,垂足为D、E,点A的坐标为(-2,5),则线段DE的长为( )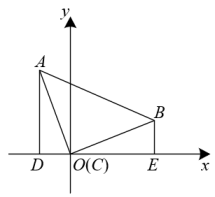 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若关于x的多项式2x3+2mx2﹣6x2-5x-1不含x2项,则m= .14. 因式分解:.15. 若关于x的方程(k﹣1)x2+x+1=0有两个实数根,那么k的取值范围是16. 如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).
 17. 如图,过⊙O外一点P向⊙O作两条切线,切点分别为A、B,若⊙O的半径为2,∠APB=60°,则图中阴影部分的面积为 .
17. 如图,过⊙O外一点P向⊙O作两条切线,切点分别为A、B,若⊙O的半径为2,∠APB=60°,则图中阴影部分的面积为 . 18. 如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是 .
18. 如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是 .
三、解答题
-
19. 定义新运算:对于任意实数a、b,都有a⊕b=2(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
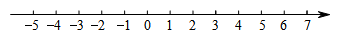 (1)、求(-2)⊕3的值;(2)、若3⊕x的值小于13,4⊕x的值大于-3,求x的取值范围,并在如图的数轴上表示出来.20. 先化简,再求值:(3a+1)(2a-3)-(6a-5)•(a-4),其中a=-2.21. 某校为了调查学生视力变化情况,从该校2008年入校的学生中抽取了部分学生进行连续三年的视力跟踪调查,将所得数据处理,制成折线统计图和扇形统计图,如图所示:
(1)、求(-2)⊕3的值;(2)、若3⊕x的值小于13,4⊕x的值大于-3,求x的取值范围,并在如图的数轴上表示出来.20. 先化简,再求值:(3a+1)(2a-3)-(6a-5)•(a-4),其中a=-2.21. 某校为了调查学生视力变化情况,从该校2008年入校的学生中抽取了部分学生进行连续三年的视力跟踪调查,将所得数据处理,制成折线统计图和扇形统计图,如图所示: (1)、该校被抽查的学生共有多少名?(2)、现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2010年有多少名学生视力合格.22. 学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?23. 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与CD交于点G.
(1)、该校被抽查的学生共有多少名?(2)、现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2010年有多少名学生视力合格.22. 学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?23. 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与CD交于点G.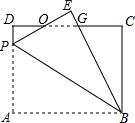 (1)、求证:AP=DG;(2)、求线段AP的长.24. 某出租汽车公司有出租车100辆,平均每天每车消耗的汽油费为80元,为了减少环境污染,市场推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装价格为4000元.公司第一次改装了部分车辆后核算:已改装后的车辆每天的燃料费占剩下的未改装车辆每天燃料费用的 , 公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下未改装车辆每天的燃料费用的.问:(1)、公司共改装了多少辆出租车?改装后的每辆出租车平均每天的燃料费比改装前的燃料费下降了百分之多少?(2)、若公司一次性将全部出租车改装,多少天后就可以从节省的燃料费中收回成本?25. 如图,已知抛物线y=-x2+bx+c与x轴相交于点A,B(4,0),与y轴相交于点C,直线y=-x+3经过点C,与x轴相交于点D.
(1)、求证:AP=DG;(2)、求线段AP的长.24. 某出租汽车公司有出租车100辆,平均每天每车消耗的汽油费为80元,为了减少环境污染,市场推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装价格为4000元.公司第一次改装了部分车辆后核算:已改装后的车辆每天的燃料费占剩下的未改装车辆每天燃料费用的 , 公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下未改装车辆每天的燃料费用的.问:(1)、公司共改装了多少辆出租车?改装后的每辆出租车平均每天的燃料费比改装前的燃料费下降了百分之多少?(2)、若公司一次性将全部出租车改装,多少天后就可以从节省的燃料费中收回成本?25. 如图,已知抛物线y=-x2+bx+c与x轴相交于点A,B(4,0),与y轴相交于点C,直线y=-x+3经过点C,与x轴相交于点D.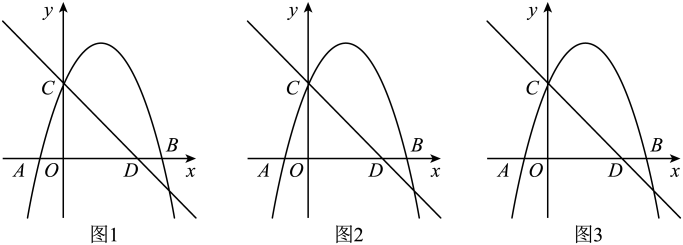 (1)、求抛物线的解析式;(2)、点P为第一象限抛物线上一点,过点P作x轴的垂线,垂足为点E,PE与线段CD相交于点G,过点G作y轴的垂线,垂足为点F,连接EF,过点G作EF的垂线,与y轴相交于点M,连接ME,MD,设△MDE的面积为S,点P的横坐标为t,求S与t的函数关系式;(3)、在(2)的条件下,过点B作直线GM的垂线,垂足为点K,若BK=OD,求:t值及点P到抛物线对称轴的距离.26. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G.
(1)、求抛物线的解析式;(2)、点P为第一象限抛物线上一点,过点P作x轴的垂线,垂足为点E,PE与线段CD相交于点G,过点G作y轴的垂线,垂足为点F,连接EF,过点G作EF的垂线,与y轴相交于点M,连接ME,MD,设△MDE的面积为S,点P的横坐标为t,求S与t的函数关系式;(3)、在(2)的条件下,过点B作直线GM的垂线,垂足为点K,若BK=OD,求:t值及点P到抛物线对称轴的距离.26. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G. (1)、求证:△ABE∽△DEF;(2)、若正方形的边长为16,求BG的长.
(1)、求证:△ABE∽△DEF;(2)、若正方形的边长为16,求BG的长.