四川省蓬安县2022年九年级下学期第二次诊断性考试数学试卷

试卷更新日期：2022-07-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上点A与点B关于原点对称，则m＝（）.

A、2 B、－2 C、 $\frac{1}{2}$ D、 $\sqrt{2}$

查看试题解析
2. 如图，△ABC是等边三角形， $A D ∥ B E$ ，若 $∠ 1 = 40 °$ ，则∠2的度数为（）

A、 $6 0^{∘}$ B、 $4 0^{∘}$ C、 $3 0^{∘}$ D、 $2 0^{∘}$

查看试题解析
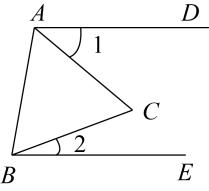3. 下列计算正确的是（）

A、 $- (a + b) = - a + b$ B、 $3 a - a = 3$ C、 $a^{6} \div a^{2} = a^{4}$ D、 ${(- 2 a^{2})}^{3} = - 6 a^{6}$

查看试题解析
4. 某校春季运会上，王雨等11名同学参加了女子百米预赛，预赛选手成绩各不相同，王雨的预赛成绩是12″3，若取前6名参加决赛，她想知道自己能否进入决赛，还需知道这11名选手百米预赛成绩的（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 如图，在△ABC中， $∠ A C B = 9 0^{∘}$ ，点D是AB的中点，将△ACD沿CD对折得△A′CD.连接 $B A^{'}$ ，连接AA′交CD于点E，若 $A B = 14 c m$ ， $B A^{'} = 4 c m$ ，则CE的长为（）

A、4cm B、5cm C、6cm D、7cm

查看试题解析
6. 已知x、y满足方程组 ${\begin{array}{l} x + 2 y = 2 m - 1 \\ 2 x + y = 5 \end{array}$ ，且x与y互为相反数，则m的值为（）

A、 $m = - 2$ B、 $m = 2$ C、 $m = - 3$ D、 $m = 3$

查看试题解析
7. 为贯彻落实“绿水青山就是金山银山”的发展理念，高坪区提出打造“森林城市”目标，绿色森林点亮城市，城市景色不断添绿.我区2019年底森林覆盖率为33.5%，在2021年底森林覆盖率达到35.6%，设我区这两年森林覆盖率的年平均增长率为x，那么可列方程为（）

A、 $33.5 % (1 + x) = 35.6 %$ B、 $33.5 % (1 + 2 x) = 35.6 %$ C、 $33.5 % {(1 + x)}^{2} = 35.6 %$ D、 $33.5 % {(1 + 2 x)}^{2} = 35.6 %$

查看试题解析
8. 如图，直线 $y = k x + b (k b \neq 0)$ 经过点P（2，1），与x，y轴分别交于点A，B，则 $\frac{1}{O A} + \frac{1}{2 O B}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、无法确定

查看试题解析
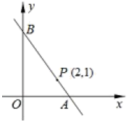9. 如图，在半径为4的扇形OAB中， $∠ A O B = 90 °$ ，点C是 $\overset{⌢}{A B}$ 上一动点，点D是OC的中点，连结AD并延长交OB于点E，则图中阴影部分面积的最小值为（）

A、 $4 π - 4$ B、 $4 π - \frac{8 \sqrt{3}}{3}$ C、 $2 π - 4$ D、 $2 π - \frac{8 \sqrt{3}}{3}$

查看试题解析
10. 如图，在等腰直角△ABC中，已知 $∠ C = 9 0^{∘}$ ， $A C = B C = 10$ ，点D是边AB上一动点，作 $∠ E D F = 4 5^{∘}$ ，两边分别交AC，BC于点E，F，则AE·BF的最大值为（）

A、10 $\sqrt{2}$ B、25 C、25 $\sqrt{2}$ D、50

查看试题解析

二、填空题

11. 若 $a > b$ ，则 $- 2 a$ $- 2 b$ ．（填 $>$ ， $=$ 或 $<$ ）

查看试题解析
12. 如图，在矩形ABCD中，点E，F分别在边AD，BC上.若四边形BEDF是菱形，若△ABE的周长为10cm，则矩形ABCD的周长为cm.

查看试题解析
13. 2022年6月22日，第31届世界大学生夏季运动会将在成都举办，成都大运会是中国西部第一次举办世界性综合运动会.成都大运会的口号为“成都成就梦想”，小明将分别写有“成”、“都”、“成”、“就”、“梦”、“想”汉字的六张卡片（这些卡片除汉字外无其他差别）背面朝上放在桌子上，混合均匀，然后随机摸出一张卡片，则恰好抽中“成”的概率为.

查看试题解析
14. 已知关于x的分式方程 $\frac{x}{x - 1} = \frac{m}{2 x - 2} + 3$ 的解是非负数，则m的取值范围是.

查看试题解析
15. 如图，在△ABC中，DC平分∠ACB， $B D ⊥ C D$ 于点D， $∠ A B D = ∠ A$ ，若 $B D = 1$ ， $A C = 7$ ，则tan∠CBD的值为.

查看试题解析
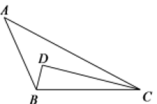16. 关于抛物线 $y = x^{2} - (2 m - 1) x + m^{2} - m$ ，与x轴交于A、B两点（A在B左侧），给出下列4个结论：①当抛物线的顶点在y轴的正半轴上时， $m = \frac{1}{2}$ ；②点P在抛物线上，当符合条件 $S_{△ P A B} = a$ （a为常数）的点有3个时，则 $a = \frac{1}{8}$ ；③当 $0 < x < \frac{1}{2}$ 时，y＜0，；④已知C（0，2），D（0，4），当 $A C + B D$ 取最小值时， $m = \frac{2}{3}$ .其中正确结论的序号是.

查看试题解析

三、解答题

17. 计算： ${(- 1)}^{2027} + 2 {(1 - π)}^{0} - | t a n 6 0^{∘} - \sqrt{4} | - \sqrt{3}$

查看试题解析
18. 如图，在△ABC中， $A B = A C$ ，点D、E在BC上， $B D = C E ， ∠ G = ∠ F$ .求证： $A F = A G$ .

查看试题解析
19. 为落实“双减”政策，丰富课外活动内容，某校九年级开展了选课走班兴趣活动.开设了演讲、篮球、唱歌、绘画四门课程，要求每位同学必须参加，且限报一门课程.在九年级随机抽取了部分样本进行了统计，并将统计结果绘成如下两幅统计图.请你结合图中所给出的信息解答下列问题：

(1)、所选样本的样本容量为，扇形统计图中“绘画”对应扇形的圆心角的大小为；

(2)、若该校九年级学生有500人，请你估计选课走班活动中，参加演讲和绘画课程的学生共有多少人？

(3)、若所选样本中参加绘画课程的男生为2人，其余为女生，现从中任选2人参加绘画展演，请用树状图或列表法求所选学生为1男1女的概率.

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - 4 k x + 3 k^{2} = 0$ .

(1)、求证：该方程总有两个实数根；

(2)、若 $k > 0$ ，且该方程的两个实数根的差为3，求k的值.

查看试题解析
21. 如图，一次函数 $y = a x + b (a \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于A（1，6），B两点， $A D ⊥ y$ 轴于点D. $B C ⊥ y$ 轴于点C， $D C = 5$ .

(1)、求该一次函数和反比例函数的解析式；

(2)、点P是DC上一点，△PAB的面积为8，求点P的坐标.

查看试题解析
22. 如图，AB是⊙O的直径，延长AB至点C，使 $B C = O B$ ， CD与⊙O相切于点D. $D E ⊥ A E$ 于点E.

(1)、求证： $O E = B E$ ；

(2)、点F是直径AB下方⊙O上的一动点（不与点A，B重合），连接FE，FC，FO.
①求 $\frac{E F}{C F}$ 的值；
②当F运动到何处时？∠OFE的度数最大，请直接写出此时∠OFE的度数.

查看试题解析
23. 某时令水果上市的时候，一果农以“线上”与“线下”相结合的方式一共销售了200箱该种水果.已知“线上”销售的每箱利润为50元.“线下”销售的每箱利润y（元）与销售量x（箱）之间的函数关系如图中线段AB.

(1)、若“线上”与“线下”销售量相同，求果农售完这200箱水果获得的总利润.

(2)、当“线下”的销售利润为4500元时，求“线下”的销售量.

(3)、实际 “线下”销售时，每箱还要支出其它相关费用m元 $(0 < m < 10)$ ，若“线上”与“线下”售完这200箱该水果所获得的最大总利润为11225元，求m的值.

查看试题解析
24. 已知正方形ABCD的边长为4，点E，F分别在AB，BC边上， $A F ⊥ D E$ ，垂足为G， $C P = A F$ 于点P，连接BP，DP，DP与BC交于点M.

(1)、求证： $A E = B F$ ；

(2)、当点E在AB上运动时，∠EDP的大小是否变化？若不变，请你求出∠EDP的度数；若变化，请你说明理由；

(3)、若 $A E = 2$ ，求MF的值.

查看试题解析
25. 如图1，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A，B两点，与y轴交于点C，已知点A的横坐标为－1，点C的纵坐标为3

(1)、求该抛物线的解析式，并写出其对称轴直线；

(2)、设点P是抛物线对称轴上一点，连接PA，将线段PA绕点P顺时针旋转 $9 0^{∘}$ ，点A的对应点为D，若点D恰好落在该抛物线上，求点P的坐标；

(3)、如图2，连接CB，若点Q是直线BC上方抛物线上一点，点M为y轴上一点，当△QBC面积最大时，求 $Q M + \frac{\sqrt{2}}{2} O M$ 的最小值.

查看试题解析