四川省绵阳市梓潼县2022年九年级教育质量监测（二诊）数学试卷

试卷更新日期：2022-07-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $| - 4 | - (- 1)$ 的最后结果是（）

A、3 B、－3 C、－5 D、5

查看试题解析
2. 下列图形均表示医疗或救援的标识，其中既是轴对称图形又是中心对称图形的是（　　）

A、医疗废物 B、中国红十字会 C、医疗卫生服务机构 D、国际急救

查看试题解析
3. 国家统计局2021年5月11日公布了第七次全国人口普查结果，全国总人口约14.1亿人，将14.1亿用科学记数法表示为（）

A、14.1×10⁸ B、1.41×10⁸ C、1.41×10⁹ D、0.141×10¹⁰

查看试题解析
4. 分别由5个大小相同的正方体组成的甲、乙两个几何体，从同一个方向看到的几何体形状图完全一致的是（）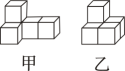

A、从正面看 B、从左面看 C、从上面看 D、以上都不对

查看试题解析
5. 已知点P（a+1， $- \frac{a}{2} + 1$ ）关于原点的对称点在第四象限，则a的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡，斜坡CD的坡度（或坡比）为 $i = 1 ： 2.4$ ，坡顶D到BC的垂直距离 $D E = 50$ 米（点A，B，C，D，E在同一平面内），在点D处测得建筑物顶A点的仰角为50°，则建筑物AB的高度约为（参考数据： $\sin 50 ° \approx 0.77$ ； $\cos 50 ° \approx 0.64$ ； $\tan 50 ° \approx 1.19$ ）

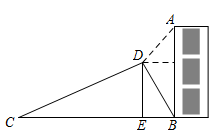A、69.2米 B、73.1米 C、80.0米 D、85.7米

查看试题解析
7. 如图，四边形ABCD中， $D C / / A B ， B C = 1 ， A B = A C = A D = 2$ 则BD的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{14}$ C、 $\sqrt{15}$ D、 $3 \sqrt{2}$

查看试题解析
8. 已知 $a 、 b 、 c$ 是自然数，且满足 $2^{a} \times 3^{b} \times 4^{c} = 192$ ，则 $a + b + c$ 的取值不可能是（　　　）

A、5 B、6 C、7 D、8

查看试题解析
9. 如图5，在反比例函数 $y = - \frac{2}{x}$ 的图象上有一动点 $A$ ，连接 $A O$ 并延长交图象的另一支于点 $B$ ，在第一象限内有一点C，满足 $A C = B C$ ，当点 $A$ 运动时，点 $C$ 始终在函数 $y = \frac{k}{x}$ 的图象上运动，若 $\tan ∠ C A B = 2$ ，则 $k$ 的值为（）

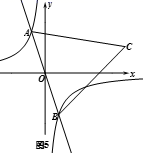A、2 B、4 C、6 D、8

查看试题解析
10. 如图，上下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为多少？（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732， $\sqrt{5}$ ≈2.236）（）

A、320cm B、395.24 cm C、431.76 cm D、480 cm

查看试题解析
11. 如图，在菱形纸片ABCD中，∠A＝60°，将纸片折叠，点A，D分别落在点 $A^{'}$ ， $D^{'}$ 处，且 $A^{'} D^{'}$ 经过点B，EF为折痕，当 $D^{^{'}} F$ ⊥CD时， $\frac{C F}{D F}$ 的值为（）

A、 $\frac{\sqrt{3} - 1}{2}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{2 \sqrt{3} - 1}{6}$ D、 $\frac{\sqrt{3} + 1}{8}$

查看试题解析
12. 关于x的方程 $x^{2} + 2 k x + 3 k = 0$ 的两个相异实根均大于-1且小于3，那么k的取值范围是（）

A、-1＜k＜0 B、k＜0 C、k＞3或k＜0 D、k＞-1

查看试题解析

二、填空题

13. 因式分解： $x^{3} y - 9 x y =$ ．

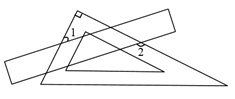
查看试题解析
14. 一把直尺与一块三角板如图放置，若 $∠ 1 = 47 °$ ，则 $∠ 2$ 的度数为.

查看试题解析
15. 如图，⊙O的弦AB垂直平分半径OC，若 $A B = \sqrt{6}$ ，则⊙O的半径为.

查看试题解析
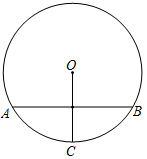16. A、B两地之间的路程为2380米，甲、乙两人分别从A、B两地出发，相向而行，已知甲先出发5分钟后，乙才出发，他们两人在A、B之间的C地相遇，相遇后，甲立即返回A地，乙继续向A地前行．甲到达A地时停止行走，乙到达A地时也停止行走，在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示，则乙到达A地时，甲与A地相距的路程是米．

查看试题解析
17. 已知x，y为实数，且满足 $x^{2} - x y + 4 y^{2} = 4$ ，记 $u = x^{2} + x y - 4 y^{2}$ 的最大值为M，最小值为m，则M+m＝.

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，分别以AB，AC，BC为边向外作正方形.连接CD，若 $s i n ∠ B C D = \frac{3}{5}$ ，则tan∠CDB的值为.

查看试题解析

三、解答题

19.

(1)、计算： $- 2^{2} + {(\frac{1}{3})}^{- 2} + | 3 - 2 \sqrt{3} | - 4 s i n 60 °$

(2)、先化简，再求值： $\frac{1}{2 a} - \frac{1}{a - b} (\frac{a - b}{2 a} - a^{2} + b^{2})$ ，其中 $a = 3 - 2 \sqrt{2}$ ， $b = 3 \sqrt{2} - 3$ .

查看试题解析
20. 202年4月23日，是第26个世界读书日.为了让校园沐浴着浓郁的书香，某学校一课外学习小组在全校随机邀请了部分同学参与问卷调查，统计同学们一个月阅读课外书的数量，并绘制了以下统计图.

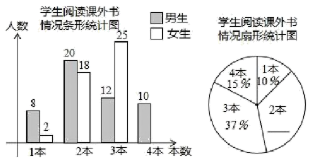
请根据图中信息解决下列问题：

(1)、共有名同学参与问卷调查；补全条形统计图和扇形统计图.

(2)、全校共有学生1500人，请估计该校学生一个月阅读2本课外书的人数约为多少；

(3)、学习小组从每一个月阅读4本课外书的同学中选取2名男生、2名女生组成一个“阅读”宣讲小组，若从4人中随机指定两人担任正、副组长，求这两人刚好是一名男生一名女生的概率.

查看试题解析
21. 已知点P在一次函数 $y = k x + b$ （k，b为常数，且 $k < 0 ， b > 0$ ）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数 $y = k x + b$ 的图象上.

(1)、k的值是；

(2)、如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数 $y = - \frac{4}{x}$ 图象交于C，D两点（点C在第二象限内），过点C作 $C E ⊥ x$ 轴于点E，记 $S_{1}$ 为四边形 $C E O B$ 的面积， $S_{2}$ 为 $△ O A B$ 的面积，若 $\frac{S_{1}}{S_{2}} = \frac{7}{9}$ ，求b的值.

查看试题解析
22. 由于受金融危机的影响，某店经销的甲型号手机今年的售价比去年每台降价500元．如果卖出相同数量的手机，那么去年销售额为8万元，今年销售额只有6万元．

(1)、今年甲型号手机每台售价为多少元？

(2)、为了提高利润，该店计划购进乙型号手机销售，已知甲型号手机每台进价为1000元，乙型号手机每台进价为800元，预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台，请问有几种进货方案？

(3)、若乙型号手机的售价为1400元，为了促销，公司决定每售出一台乙型号手机，返还顾客现金a元，而甲型号手机仍按今年的售价销售，要使（2）中所有方案获利相同，a应取何值？

查看试题解析
23. 图，在 $△ A B C$ 中，AB＝AC，⊙O是 $△ A B C$ 的外接圆，点D在⊙O上且∠BCD＝∠ACB，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF.

(1)、求证：AF是⊙O的切线；

(2)、若点G是 $△ A C D$ 的内心， $B C \cdot B E = 25$ ，求BG的长.

查看试题解析
24. 如图1，已知直线y=kx与抛物线 $y = - \frac{4}{27} x^{2} + \frac{22}{3}$ 交于点A（3，6）.

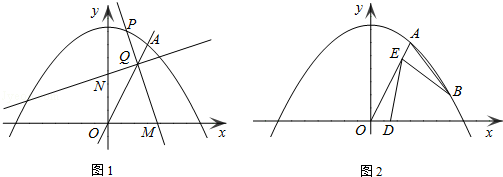(1)、求直线y=kx的解析式和线段OA的长度；

(2)、点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N.试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；

(3)、如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD.继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？

查看试题解析
25. 如图，矩形ABCD中，AB=6，BC=2 $\sqrt{3}$ ，点O是AB的中点，点P在AB的延长线上，且BP=3.一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒（t≥0）.

(1)、当等边△EFG的边FG恰好经过点C时，求运动时间t的值；

(2)、在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；

(3)、设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由.

查看试题解析