四川省眉山市彭山区2022年九年级一诊数学试卷
试卷更新日期:2022-07-26 类型:中考模拟
一、单选题
-
1. ﹣ 的相反数是( )A、﹣ B、﹣ C、 D、2. 2020年6月23日,我国的北斗卫星导航系统(BDS)星座部署完成,其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为( )A、 0.215×108 B、2.15×107 C、2.15×106 D、21.5×1063. 如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
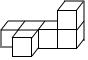 A、
A、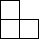 B、
B、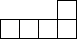 C、
C、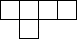 D、
D、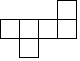 4. 下列运算正确的是( )A、 B、 C、 D、5. 为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.A、200 B、300 C、400 D、5006. 如图,将绕点A逆时针旋转一定角度得到.若 , , 且 , 的度数为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 为了估计某地区梅花鹿的数量,先捕捉20只梅花鹿做上标记,然后放走,待有标记的梅花鹿完全混合于鹿群后,第二次捕捉100只梅花鹿,发现其中5只有标记.估计这个地区的梅花鹿的数量约有( )只.A、200 B、300 C、400 D、5006. 如图,将绕点A逆时针旋转一定角度得到.若 , , 且 , 的度数为( ) A、65° B、70° C、75° D、85°7. 如图,△ABC中,∠A=120°,若BM,CM分别是△ABC的外角平分线,则∠M的余弦值是( )
A、65° B、70° C、75° D、85°7. 如图,△ABC中,∠A=120°,若BM,CM分别是△ABC的外角平分线,则∠M的余弦值是( )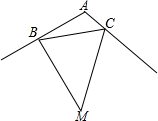 A、 B、 C、 D、8. 若二元一次方程组 的解为 则 的值是( )A、3 B、1 C、 D、29. 如图, 为 的直径,C、D为 上两点, ,则 的长度为( )
A、 B、 C、 D、8. 若二元一次方程组 的解为 则 的值是( )A、3 B、1 C、 D、29. 如图, 为 的直径,C、D为 上两点, ,则 的长度为( ) A、3 B、4 C、5 D、610. 若一元二次方程x2−4x−4m=0有两个不相等的实数根,则正比例函数y=(m+2)x的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限11. 若关于x的一元一次不等式结 的解集为 ;且关于 的分式方程 有正整数解,则所有满足条件的整数a的值之积是( )A、7 B、-14 C、28 D、-5612. 如图,在等边三角形ABC的AC,BC边上分别任取一点P,Q,且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP•AQ;④若AB=3,则OC的最小值为 , 其中正确的是( )
A、3 B、4 C、5 D、610. 若一元二次方程x2−4x−4m=0有两个不相等的实数根,则正比例函数y=(m+2)x的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限11. 若关于x的一元一次不等式结 的解集为 ;且关于 的分式方程 有正整数解,则所有满足条件的整数a的值之积是( )A、7 B、-14 C、28 D、-5612. 如图,在等边三角形ABC的AC,BC边上分别任取一点P,Q,且AP=CQ,AQ、BP相交于点O.下列四个结论:①若PC=2AP,则BO=6OP;②若BC=8,BP=7,则PC=5;③AP2=OP•AQ;④若AB=3,则OC的最小值为 , 其中正确的是( ) A、①②④ B、①③④ C、②③④ D、①②③
A、①②④ B、①③④ C、②③④ D、①②③二、填空题
-
13. 因式分解: .14. 函数y= 的自变量x的取值范围是 .15. 如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°, 则此圆锥高 OC 的长度是 .
 16. 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:①分别以点B、C为圆心,大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D;③连接BD.若AC=8,则BD的长为.
16. 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:①分别以点B、C为圆心,大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D;③连接BD.若AC=8,则BD的长为. 17. 观察下列等式:
17. 观察下列等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第5个等式:;…
根据以上规律,写出你猜想的第n个等式(用含n的等式表示)
18. 如图,点E是菱形ABCD边AB的中点,点F为边AD上一动点,连接EF,将△AEF沿直线EF折叠得到△A'EF,连接A'D,A'C.已知 BC=4,∠B=120°,当△A'CD为直角三角形时,线段AF的长为.
三、解答题
-
19. 计算:.20. 若 , 求代数式的值.21. 目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
 (1)、此次抽样调查中,共调查了多少名中学生家长;(2)、求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)、在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.22. 如图,已知直线y=x+1与双曲线y=交于A(a,2)、B(−2,b)两点,过点A作AC⊥x轴于点C.
(1)、此次抽样调查中,共调查了多少名中学生家长;(2)、求出图2中扇形C所对的圆心角的度数,并将图1补充完整;(3)、在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.22. 如图,已知直线y=x+1与双曲线y=交于A(a,2)、B(−2,b)两点,过点A作AC⊥x轴于点C. (1)、A点的坐标为 , B点的坐标为 , 双曲线解析式为.(2)、直接写出关于x的不等式:的解集;(3)、若点P在直线上,是否存在点P,使.若存在,请求出此时点P的坐标,若不存在,请说明理由.23. 周末小亮一家到水上乐园游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到达A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73
(1)、A点的坐标为 , B点的坐标为 , 双曲线解析式为.(2)、直接写出关于x的不等式:的解集;(3)、若点P在直线上,是否存在点P,使.若存在,请求出此时点P的坐标,若不存在,请说明理由.23. 周末小亮一家到水上乐园游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到达A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73 24. 由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车每辆的进价相同).第一次用275万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用191万元购进甲型号汽车14辆和乙型号汽车25辆.(1)、求甲、乙两种型号汽车每辆的进价;(2)、经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车5.8万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的辆数不少于甲型号汽车辆数的2倍,若两种型号汽车每辆的进价与售价均不变,请你求出获利最大的购买方案,并求出最大利润.25. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
24. 由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车每辆的进价相同).第一次用275万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用191万元购进甲型号汽车14辆和乙型号汽车25辆.(1)、求甲、乙两种型号汽车每辆的进价;(2)、经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车5.8万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的辆数不少于甲型号汽车辆数的2倍,若两种型号汽车每辆的进价与售价均不变,请你求出获利最大的购买方案,并求出最大利润.25. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.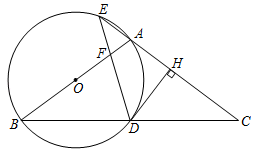 (1)、求证:DH是⊙O的切线;(2)、若点A为EH的中点,求的值;(3)、若EA=EF=2,求⊙O的半径.26. 如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为.
(1)、求证:DH是⊙O的切线;(2)、若点A为EH的中点,求的值;(3)、若EA=EF=2,求⊙O的半径.26. 如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.直线l与抛物线交于A,D两点,与y轴交于点E,点D的坐标为.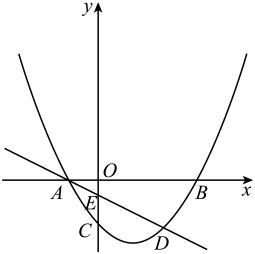 (1)、请直接写出A,B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 , 过点P作轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 , 求点Q的坐标.
(1)、请直接写出A,B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 , 过点P作轴,垂足为M.PM与直线l交于点N,当点N是线段PM的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 , 求点Q的坐标.