四川省乐山市峨边县2022年九年级调查研究考试（一诊）数学试卷

试卷更新日期：2022-07-26 类型：中考模拟

进入出卷网下载

一、单选题

1. -4的相反数是（）

A、 $\frac{1}{4}$ B、 $- \frac{1}{4}$ C、4 D、-4

查看试题解析
2. 已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为（）

A、8.23×10^﹣⁶ B、8.23×10^﹣⁷ C、8.23×10⁶ D、8.23×10⁷

查看试题解析
3. 如图是由5个完全相同的小正方体组成的几何体，则该几何体的左视图是（）

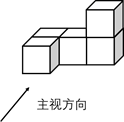A、 B、 C、 D、

查看试题解析
4. 如图，△ABC中，AB=6，AC=8，∠ABC与∠ACB的平分线BD、CD交于点D.过点D作EF∥BC，分别交AB，AC于点E，F，则△AEF的周长为（）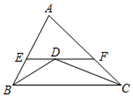

A、12 B、13 C、14 D、15

查看试题解析
5. 下列计算正确的是（）

A、7ab﹣5a＝2b B、（a+ $\frac{1}{a}$ ）²＝a²+ $\frac{1}{a^{2}}$ C、（﹣3a²b）²＝6a⁴b² D、3a²b÷b＝3a²

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x - 6 > 0 \\ 4 - x < - 1 \end{array}$ 的解集是（）

A、 $x > 5$ B、 $3 < x < 5$ C、 $x < 5$ D、 $x > - 5$

查看试题解析
7. 已知 $10^{a} = 20$ ， $100^{b} = 50$ ，则 $\frac{1}{2} a + b + \frac{3}{2}$ 的值是（）

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{9}{2}$

查看试题解析
8. 如图，在菱形 $A B C D$ 中，P是对角线 $A C$ 上一动点，过点P作 $P E ⊥ B C$ 于点E. $P F ⊥ A B$ 于点F.若菱形 $A B C D$ 的周长为20，面积为24，则 $P E + P F$ 的值为（）

A、4 B、 $\frac{24}{5}$ C、6 D、 $\frac{48}{5}$

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，AC＝BC ，点O在AB上，经过点A的⊙O与BC相切于点D ，交AB于点E ，若CD＝ $\sqrt{2}$ ，则图中阴影部分面积为（）

A、4﹣ $\frac{π}{2}$ B、2﹣ $\frac{π}{2}$ C、2﹣π D、1﹣ $\frac{π}{4}$

查看试题解析
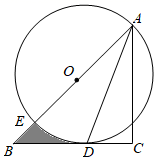10. 如图是二次函数y=ax²+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：
①abc＜0；
②2a﹣b=0；
③4a+2b+c＜0；
④若（﹣5，y₁），（ $\frac{5}{2}$ ，y₂）是抛物线上两点，则y₁＞y₂ ．
其中说法正确的是（）

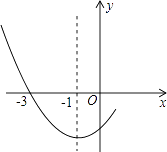A、①② B、②③ C、①②④ D、②③④

查看试题解析

二、填空题

11. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 分解因式： ${2a}^{2} - 4a + 2 =$ ．

查看试题解析
13. 三角形两边的长分别为2和5，第三边的长是方程 $x^{2} - 8 x + 15 = 0$ 的根，则该三角形的周长为 .

查看试题解析
14. 如图，由边长为1的小正方形组成的网格中，点A ， B ， C都在格点上，以 $A B$ 为直径的圆经过点C和点D ，则 $\tan ∠ A D C =$ ．

查看试题解析
15. 如图所示，在数轴上，点 $A$ 表示1，现将点 $A$ 沿轴做如下移动，第一次点 $A$ 向左移动3个单位长度到达点 $A_{1}$ ，第二次将点 $A_{1}$ 向右移动6个单位长度到达点 $A_{2}$ ，第三次将点 $A_{2}$ 向左移动9个单位长度到达点 $A_{3}$ ，按照这种移动规律移动下去，第 $n$ 次移动到点 $A_{n}$ ，如果点 $A_{n}$ 与原点的距离不小于20，那么 $n$ 的最小值是．

查看试题解析
16.
在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒 $\sqrt{2}$ 个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒，当t为时，△PQB为直角三角形．

查看试题解析

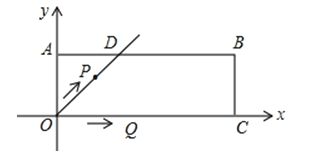
三、解答题

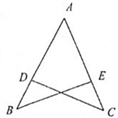
17. 计算： $\sqrt{8}$ ﹣2sin30°﹣|1﹣ $\sqrt{2}$ |+（ $\frac{1}{2}$ ）^﹣²﹣（π﹣2020）⁰ ．

查看试题解析
18. 如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C．求证：BD=CE.

查看试题解析
19. 先化简，再求值： $\frac{4 a}{a^{2} - 9} \div (1 + \frac{a - 3}{a + 3})$ ，其中a $= \sqrt{2} + 3$ .

查看试题解析
20. 为引导学生知史爱党、知史爱国，某中学组织全校学生进行“党史知识”竞赛，该校德育处随机抽取部分学生的竞赛成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格，并绘制成两幅不完整的统计图.

根据以上信息，解答下列问题：

(1)、德育处一共随机抽取了名学生的竞赛成绩；在扇形统计图中，表示“一般”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、该校共有1400名学生，估计该校大约有多少名学生在这次竞赛中成绩优秀？

(4)、德育处决定从本次竞赛成绩前四名学生甲、乙、丙、丁中，随机抽取2名同学参加全市“党史知识”竞赛，请用树状图或列表法求恰好选中甲和乙的概率.

查看试题解析
21. 如图，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x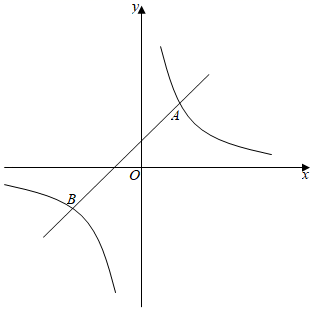}$ 的图象相交于 $A (1 ， 2)$ 、 $B (- 2 ， n)$ 两点.

(1)、求一次函数和反比例函数的解析式；

(2)、根据图象，直接写出满足 $k_{1} x + b > \frac{k_{2}}{x}$ 的 $x$ 的取值范围；

(3)、若点 $P$ 在线段 $A B$ 上，且 $S_{Δ A O P} ： S_{Δ B O P} = 1 ： 4$ ，求点 $P$ 的坐标.

查看试题解析
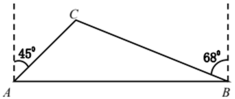22. 为推进我县中心城区污水系统综合治理项目，需要从如图A，B两地向C地新建AC，BC两条笔直的污水收集管道，现测得C地在A地北偏东45°方向上，在B地北偏西68°方向上，AB的距离为7km，求新建管道的总长度.（结果精确到0.1km， $s i n 22 ° \approx 0.37$ ， $c o s 22 ° \approx 0.93$ ， $t a n 22 ° \approx 0.40$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
23. “节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：

(1)、A型自行车去年每辆售价多少元；

(2)、该车行今年计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．已知，A型车和B型车的进货价格分别为1500元和1800元，计划B型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多．

查看试题解析
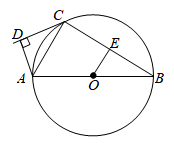24. 如图，在半径为5cm的 $⊙ O$ 中，AB是 $⊙ O$ 的直径，CD是过 $⊙ O$ 上点C的直线，且 $A D ⊥ D C$ 于点D，AC平分 $∠ B A D$ ，E是BC的中点， $O E = 3 cm$ .

(1)、求证：CD是 $⊙ O$ 的切线；

(2)、求AD的长，

查看试题解析
25. 模型探究：如图1，D、E、F分别为 $△ A B C$ 三边BC、AB、AC上的点，且 $∠ B = ∠ C = ∠ E D F = a$ .
（1） $△ B D E$ 与 $△ C F D$ 相似吗？请说明理由；
模型应用： $△ A B C$ 为等边三角形，其边长为8，E为AB边上一点，F为射线AC上一点，将 $△ A E F$ 沿EF翻折，使A点落在射线CB上的点D处，且 $B D = 2$ .

(1)、如图2，当点D在线段BC上时，求 $\frac{A E}{A F}$ 的值；

(2)、如图3，当点D落在线段CB的延长线上时，求 $△ B D E$ 与 $△ C F D$ 的周长之比.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 2$ 交x轴于A，B两点，交y轴于点C，且 $O A = 2 O C = 8 O B$ .点P是第三象限内抛物线上的一动点.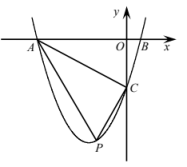

(1)、求此抛物线的表达式；

(2)、若PC//AB，求点P的坐标；

(3)、连接AC，求 $△ P A C$ 面积的最大值及此时点P的坐标.

查看试题解析