2022-2023学年浙教版数学九年级下册3.4 简单几何体的表面展开图 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为( ).
 A、 B、12π C、 D、24π2. 如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( )
A、 B、12π C、 D、24π2. 如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( ) A、130cm2 B、65πcm2 C、60πcm2 D、30cm23. 底面半径为3,高为4的圆锥侧面积为( )A、15π B、20π C、25π D、30π4. 圆锥的母线长为10,底面半径为3,则这个圆锥的侧面积为( )A、15π B、30π C、39π D、60π5. 赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )
A、130cm2 B、65πcm2 C、60πcm2 D、30cm23. 底面半径为3,高为4的圆锥侧面积为( )A、15π B、20π C、25π D、30π4. 圆锥的母线长为10,底面半径为3,则这个圆锥的侧面积为( )A、15π B、30π C、39π D、60π5. 赤峰市某青少年宫门前有一座正方体雕塑,它的每个面上都有一个汉字,如图是该正方体模型的展开图,那么在正方体中,与“英”字所在面相对的面上的汉字是( )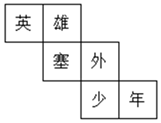 A、塞 B、外 C、少 D、年6. 如图,已知圆锥侧面展开图的扇形面积为65 cm2,扇形的弧长为10 cm,则圆锥母线长是( )
A、塞 B、外 C、少 D、年6. 如图,已知圆锥侧面展开图的扇形面积为65 cm2,扇形的弧长为10 cm,则圆锥母线长是( ) A、5cm B、10cm C、12cm D、13cm7. 如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )
A、5cm B、10cm C、12cm D、13cm7. 如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )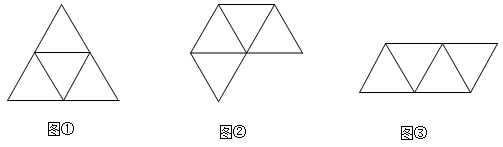 A、仅图① B、图①和图② C、图②和图③ D、图①和图③8. 已知圆锥的底面半径为3cm,高为4cm,则这个圆锥的侧面积为( )A、30π B、24π C、15π D、12π9. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )
A、仅图① B、图①和图② C、图②和图③ D、图①和图③8. 已知圆锥的底面半径为3cm,高为4cm,则这个圆锥的侧面积为( )A、30π B、24π C、15π D、12π9. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )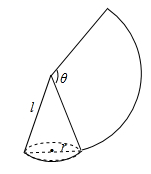 A、10 B、 C、6 D、810. 把如图所示的正方形展开,得到的平面展开图可以是( )
A、10 B、 C、6 D、810. 把如图所示的正方形展开,得到的平面展开图可以是( )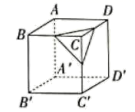 A、
A、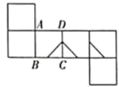 B、
B、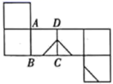 C、
C、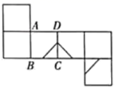 D、
D、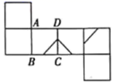
二、填空题
-
11. 如图,从一块直径是的圆形铁皮上剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径为m.
 12. 半径为10cm,母线长为15cm的圆锥的侧面积为.13. 已知圆锥的底面半径为 ,母线长为 ,则它的侧面展开图的面积为.14. 圆锥的底面圆半径为3,高为4,则圆锥侧面展开扇形图的圆心角的度数是.15. 一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是点.
12. 半径为10cm,母线长为15cm的圆锥的侧面积为.13. 已知圆锥的底面半径为 ,母线长为 ,则它的侧面展开图的面积为.14. 圆锥的底面圆半径为3,高为4,则圆锥侧面展开扇形图的圆心角的度数是.15. 一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是点.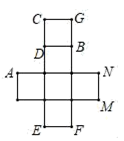 16. 已知圆锥的侧面积为 ,底面半径为4,则该圆锥的母线等于.
16. 已知圆锥的侧面积为 ,底面半径为4,则该圆锥的母线等于.三、解答题
-
17. 如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),求该圆锥底面圆的面积.(结果保留π)
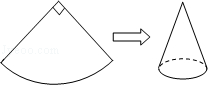 18. 如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)
18. 如图是某圆锥的三视图,请根据图中尺寸计算该圆锥的全面积.(结果保留3个有效数字)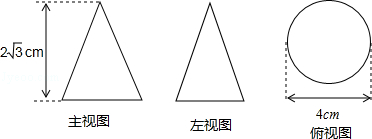 19. 如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
19. 如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长. 20. 如图所示,在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°,求光源离地面的垂直高度SO.(精确到0.1m;
20. 如图所示,在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°,求光源离地面的垂直高度SO.(精确到0.1m;=1. 414, =1.732, =2.236,以上数据供参考)
 21. 一个圆锥的侧面展开图是半径为 ,圆心角为120°的扇形,求:
21. 一个圆锥的侧面展开图是半径为 ,圆心角为120°的扇形,求: (1)、圆锥的底面半径;(2)、圆锥的全面积.22. 如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)、圆锥的底面半径;(2)、圆锥的全面积.22. 如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题: (1)、面“学”的对面是面什么?(2)、图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
(1)、面“学”的对面是面什么?(2)、图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
