（北师大版）2022-2023学年度第一学期九年级数学4.6 利用相似三角形测高 同步测试
试卷更新日期：2022-07-25 类型：同步测试
一、单选题
-
1. 小莹同学的身高为1.6米，某一时刻她在阳光下的影长为3.2米，与她邻近的一棵树的影长为8米，则这棵树的高为（ ）A、3.2米 B、3米 C、4米 D、4.2米2. 如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB//CD，AB=2米，CD=5米，点P到CD的距离是4米，则P到AB的距离为（ ）
A、2.5米 B、1.6米 C、1.5米 D、1.2 米3. 如图，图1是装了液体的高脚杯，加入一些液体后如图2所示，则此时液面AB为（ ）
A、5.6cm B、6.4cm C、8cm D、10cm4. 如图，在 中，点 在BC边上，连结DE并延长交AB的延长线于点 .若 ，则 与 的周长之比为（ ）
A、1：3 B、3：7 C、4：7 D、3：45. 如图，身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时，发现自己在地面上的影子CE的长是2米，则路灯AB的高为（ ）
A、5米 B、6.4米 C、8米 D、10米6. 如图，小芳和爸爸正在散步，爸爸身高1.8m，他在地面上的影长为2.1m．若小芳身高只有1.2m，则她的影长为（ ）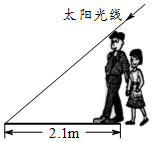
A、1.2m B、1.4m C、1.6m D、1.8m7. 在科学小实验中，一个边长为30cm正方体小木块沿着一个斜面下滑，其轴截面如图所示，初始状态，正方形的一个顶点与斜坡上的点P重合，点P的高度PF=40cm，离斜坡底端的水平距离EF=80cm，正方形下滑后，点B的对应点B与初始状态的顶点A的高度相同，则正方形下滑的距离（即AA’的长度）是（ ）cm.
A、40 B、60 C、 D、8. 如图，为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组根据光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子水平放置在离树底B端8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=3.2米，观察者目高CD=1.6米，则树AB的高度约为（ ）
A、4.2米 B、4.8米 C、6.4米 D、16.8米9. 如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2米，旗杆底部与平面镜的水平距离为12米，若小明的眼晴与地面的距离为1.5米，则旗杆的高度为（ ）
A、9 B、12 C、14 D、1810. 如图，小明在A时测得某树的影长为8m，B时又测得该树的影长为2m，若两次日照的光线互相垂直，则树的高度为（ ）m．
A、2 B、4 C、6 D、8二、填空题
-
11. 如图，小明为了测量树的高度CD，他在与树根同一水平面上的B处放置一块平面镜，然后他站在A处刚好能从镜中看到树顶D，已知A、B、C三点在同一直线上，且AB＝2m，BC＝8m．他的眼睛离地面的高度1.6m，则树的高度CD为m．
12. 如图，是小莹设计用手电来测量某古城墙高度的示意图．在点P处放一水平的平面镜，光线从点A出发经平面镜反射后，刚好射到古城墙CD的顶端C处．已知AB⊥BD， ． 且测得米，米，PD=12米，那么该古墙的高度是米．
13. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm．他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像．蜡烛应放在距离纸筒 cm的地方．
14. 某户外遮阳棚如图1，其截面结构示意图如图2所示.支撑柱AB上地面，AB=120 cm，Р是支撑柱AB上一动点，伞杆CP可绕着中点E旋转，CD=CP=40 cm，斜拉杆AE可绕点A旋转，AE= CP．若∠APE=30°，则BP=cm；伞展开长 PD==300cm，若A，C，D在同一条直线上，某时太阳光线恰好与地面垂直，则PD落到地面的阴影长为cm.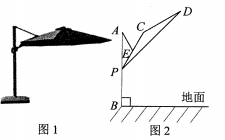
15. 如图，某时刻阳光通过窗口AB照射到室内，在地面上留下4米宽的“亮区”DE，光线与地面所成的角（如∠BEC）的正切值是 ， 那么窗口的高AB等于米．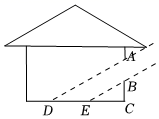
三、解答题
-
16. 如图，△ABC是一块锐角三角形余料，边BC＝120mm，高AD＝80mm，要把它加工成矩形零件PQMN，使一边在BC上，其余两个顶点分别在边AB、AC上.若这个矩形的边PN∶PQ＝1∶2，则这个矩形的长、宽各是多少？
17. 下表是小明填写的实践报告的部分内容，请你借助小明的测量数据，计算小河的宽度AB.题目
测量小河的宽度
测量目标示意图
相关数据
BCDE，BC＝1m，DE＝1.5m，BD＝5m
18. 如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞.工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM＝1千米、AN＝1.8千米，AB＝54米、BC＝45米、AC＝30米，求M、N两点之间的直线距离.
19. 如图，有一把剪刀，AB＝ BC，DB＝ BE，有一长方体，宽PQ＝10cm，想用剪刀的A、D两点夹住P、Q两点，那么手握的位置点C，点E的距离应该是多少cm？
20. 小强在地面 处放一面镜子，刚好能从镜子中看到教学楼的顶端 此时 米， 米．已知眼睛距离地面的高度 米，请计算出教学楼的高度．（根据光的反射定律，反射角等于入射角）
21. 如图，为了估计河的宽度，我们可以在河对岸选定一个目标点A，在近岸取点B，使AB与河岸垂直，在近岸取点C，E，使BC⊥AB，CE⊥BC，AE与BC交于点D．已测得BD＝40m，DC＝20m，EC＝24m，求河宽AB．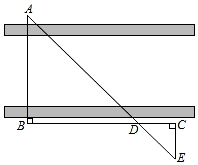
22. 如图，比例规是一种画图工具，它由长度相等的两脚AD和BC交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使 ， ），然后张开两脚，使A ， B两个尖端分别在线段l的两个端点上，这时CD与AB有什么关系？为什么？
23. 如图所示，AD、BC为两路灯，身高相同的小明、小亮站在两路灯杆之间，两人相距6.5m，小明站在P处，小亮站在Q处，小明在路灯C下的影长为2m，已知小明身高1.8m，路灯BC高9m．小明在路灯BC下的影子顶部恰好位于路灯DA的正下方，小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方．
①计算小亮在路灯D下的影长；
②计算建筑物AD的高．
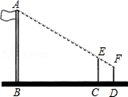
24. 在一次数学活动课上，小芳到操场上测量旗杆的高度，她的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，利用她所测数据，求旗杆的高.