(北师大版)2022-2023学年度第一学期九年级数学4.5 相似三角形判定定理的证明 同步测试
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )
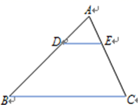 A、 B、 C、 D、2. 如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )
A、 B、 C、 D、2. 如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是( )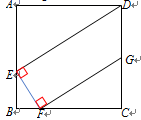 A、4 B、 C、 D、53. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )
A、4 B、 C、 D、53. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )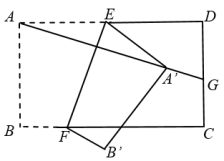 A、 B、 C、 D、4. 如图平行四边形ABCD中,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则( )
A、 B、 C、 D、4. 如图平行四边形ABCD中,F为BC中点,延长AD至E,使 , 连结EF交DC于点G,则( ) A、2∶3 B、4∶9 C、9∶4 D、3∶25. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( )
A、2∶3 B、4∶9 C、9∶4 D、3∶25. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( ) A、 B、 C、 D、6. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )
A、 B、 C、 D、6. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )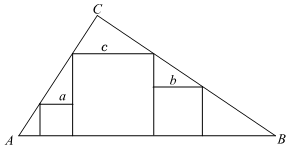 A、4 B、 C、5 D、67. 如图,△ABC的中线AD、BE相交于点F,过点E作EG∥AD交BC于点G,则EG∶AF的值是( )
A、4 B、 C、5 D、67. 如图,△ABC的中线AD、BE相交于点F,过点E作EG∥AD交BC于点G,则EG∶AF的值是( ) A、 B、 C、 D、8. 如图,已知E,F分别为正方形ABCD的边AB、BC的中点,AF与DE交于点M,则下列结论:①AF⊥DE;②;③AM=MF;④ . 其中正确的结论有( )
A、 B、 C、 D、8. 如图,已知E,F分别为正方形ABCD的边AB、BC的中点,AF与DE交于点M,则下列结论:①AF⊥DE;②;③AM=MF;④ . 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个9. 如图,将△ABC绕点C顺时针旋转α得到△DEC,此时点D落在边AB上,且DE垂直平分BC,则的值是( )
A、4个 B、3个 C、2个 D、1个9. 如图,将△ABC绕点C顺时针旋转α得到△DEC,此时点D落在边AB上,且DE垂直平分BC,则的值是( ) A、 B、 C、 D、10. 如图,矩形中, , 以B为圆心,以为半径画圆交边于点E,点P是弧上的一个动点,连结 , 则的最小值为( )
A、 B、 C、 D、10. 如图,矩形中, , 以B为圆心,以为半径画圆交边于点E,点P是弧上的一个动点,连结 , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知距离为6的两条平行线 与 分别交于 两点 为直径,且与 不垂直), D为 上一点, 过 作 的平行线 交 于点 , 若 , 则 的长为 .
 12. 如图,在△ABC中, ,CD平分 .若AD=2,BD=3,AC的长为.
12. 如图,在△ABC中, ,CD平分 .若AD=2,BD=3,AC的长为.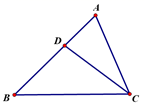 13. 如图,l1∥l2∥l3 , 若AB=2,BC=3,AD=1,CF=4,则BE的长为.
13. 如图,l1∥l2∥l3 , 若AB=2,BC=3,AD=1,CF=4,则BE的长为. 14. 如图,将△ABC沿直线AD翻折,使点B与AC边上的点E重合,若AB=AD=4,AC=6,则DC=.
14. 如图,将△ABC沿直线AD翻折,使点B与AC边上的点E重合,若AB=AD=4,AC=6,则DC=. 15. 如图,在四边形ABCD中,AD//BC,∠BAD=90°,且对角线BD⊥DC,AD=4,BC=9,则BD的长为 .
15. 如图,在四边形ABCD中,AD//BC,∠BAD=90°,且对角线BD⊥DC,AD=4,BC=9,则BD的长为 .
三、解答题
-
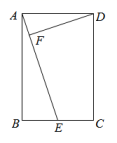
16. 如图,在矩形ABCD中,E为BC的中点,DF⊥AE ,垂足为F,AB=6,BC=4,求AE,DF的长.
 17. 如图,在梯形中, , 点在线段上,与相交于点 , 与的延长线相交于点 , 已知 , , . 求、的长.
17. 如图,在梯形中, , 点在线段上,与相交于点 , 与的延长线相交于点 , 已知 , , . 求、的长.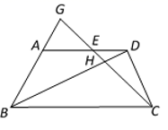 18. 如图,在平行四边形ABCD中,点E是AB的中点.CE和BD交于点O,若S△EOB=1,求四边形AEOD的面积.
18. 如图,在平行四边形ABCD中,点E是AB的中点.CE和BD交于点O,若S△EOB=1,求四边形AEOD的面积. 19. 如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
19. 如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.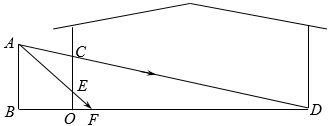 20. 已知: 中, 为 上的中线,点E在 上,且 ,射线 交 于点F.求 的值.
20. 已知: 中, 为 上的中线,点E在 上,且 ,射线 交 于点F.求 的值.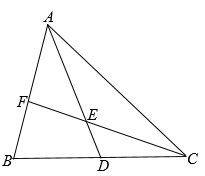 21. 如图,D、E分别是△ABC的边AC、AB上的点,AE=6,AC=10,BC=15,且 , 求DE的长.
21. 如图,D、E分别是△ABC的边AC、AB上的点,AE=6,AC=10,BC=15,且 , 求DE的长.


