2022-2023学年浙教版数学九年级下册2.3 三角形的内切圆 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
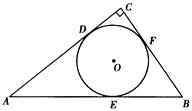
1. 下列命题正确的是( )A、三角形的内切圆圆心到三角形三个顶点的距离相等 B、对角线互相垂直平分的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、顺次连接四边形各边中点所得四边形是平行四边形2. 如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )
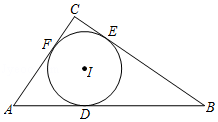
 A、 B、 C、 D、3. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )
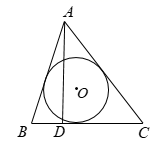
A、 B、 C、 D、3. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )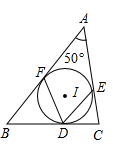 A、55° B、60° C、65° D、70°4. 已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )A、4 B、3 C、2 D、15. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A、55° B、60° C、65° D、70°4. 已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )A、4 B、3 C、2 D、15. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )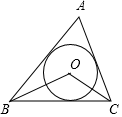 A、120° B、125° C、130° D、135°6. 如图,在△ABC中,∠BAC的平分线AD与∠ACB的平分线CE交于点O,下列说法正确的是( )
A、120° B、125° C、130° D、135°6. 如图,在△ABC中,∠BAC的平分线AD与∠ACB的平分线CE交于点O,下列说法正确的是( )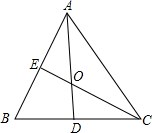 A、点O是△ABC的内切圆的圆心 B、CE⊥AB C、△ABC的内切圆经过D,E两点 D、AO=CO7. 根据尺规作图的痕迹,可以判定点O为 内心的是( )A、
A、点O是△ABC的内切圆的圆心 B、CE⊥AB C、△ABC的内切圆经过D,E两点 D、AO=CO7. 根据尺规作图的痕迹,可以判定点O为 内心的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,弓形 中, , .若点 在优弧 上由点 移动到点 ,记 的内心为 ,点 随点 的移动所经过的路径长为( ).
8. 如图,弓形 中, , .若点 在优弧 上由点 移动到点 ,记 的内心为 ,点 随点 的移动所经过的路径长为( ).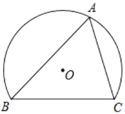 A、 B、 C、 D、9. 如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:
A、 B、 C、 D、9. 如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AC于点M,N;
②分别以M,N为圆心,以大于 MN的长为半径作弧,两弧交于点E;
③作射线AE;
④以同样的方法作射线BF,AE交BF于点O,连结OC,则OC为( )
 A、2 B、2 C、 D、110. 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( )
A、2 B、2 C、 D、110. 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( ) A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题
-
11. 如图,△ABC的内切圆与三边分别切于点D,E,F,若∠C=90°,AD=3,BD=5,则△ABC的面积为.
 12. 如图,在 中, , , , 为 的内切圆,点D是斜边AB的中点,则 .
12. 如图,在 中, , , , 为 的内切圆,点D是斜边AB的中点,则 .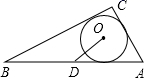 13. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.14. 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD= ,那么△ABC的内切圆半径为
13. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.14. 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD= ,那么△ABC的内切圆半径为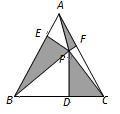 15. 如图,△ABC,AC=3,BC=4,∠C=90°,⊙O为△ABC的内切圆,与三边的切点分别为D、E、F,则⊙O的面积为(结果保留π)
15. 如图,△ABC,AC=3,BC=4,∠C=90°,⊙O为△ABC的内切圆,与三边的切点分别为D、E、F,则⊙O的面积为(结果保留π) 16. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为 , , ,…, ,则 =.
16. 如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为 , , ,…, ,则 =.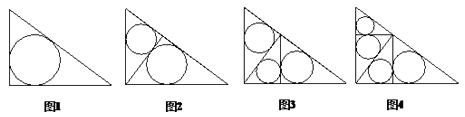
三、解答题
-
17. 如图,I是△ABC的内心,AI的延长线交△ABC的外接圆于点D.DB与DI相等吗?为什么?
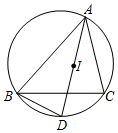 18. 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
18. 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.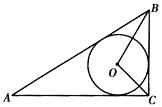 19. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
19. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.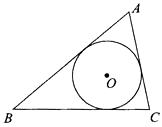 20. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60°,求弦AB的长.
20. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60°,求弦AB的长.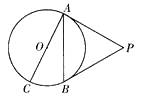 21. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
21. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.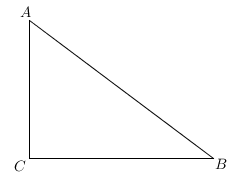 (1)、尺规作图:作三角形ABC的内切圆⊙O,⊙O分别与AB、BC、CA相切于点D、E、F保留作图痕迹,不写作法.(2)、求⊙O的半径r.22. 在平面直角坐标系中,边长为1的正方形OABC的两个顶点A,C分别在y轴、x轴的正半轴上,点O是原点.现在将正方形OABC绕原点O顺时针旋转,当点A第一次落在直线y=x上时停止.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N。
(1)、尺规作图:作三角形ABC的内切圆⊙O,⊙O分别与AB、BC、CA相切于点D、E、F保留作图痕迹,不写作法.(2)、求⊙O的半径r.22. 在平面直角坐标系中,边长为1的正方形OABC的两个顶点A,C分别在y轴、x轴的正半轴上,点O是原点.现在将正方形OABC绕原点O顺时针旋转,当点A第一次落在直线y=x上时停止.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N。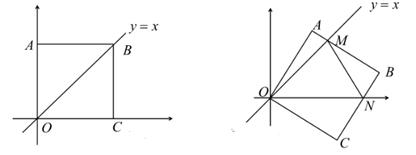 (1)、若点A( ,b),求此时点C的坐标及b的值(2)、若△MNB的周长是p,在旋转过程中,p值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;(3)、设MN=m,当m为何值时△OMN的面积最小,最小值是多少?并直接写出此时△MNB内切圆半径。
(1)、若点A( ,b),求此时点C的坐标及b的值(2)、若△MNB的周长是p,在旋转过程中,p值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;(3)、设MN=m,当m为何值时△OMN的面积最小,最小值是多少?并直接写出此时△MNB内切圆半径。