2022-2023学年浙教版数学九年级下册2.1 直线和圆的位置关系 同步练习
试卷更新日期：2022-07-25 类型：同步测试
一、单选题
-
1. 如图，若的半径为5，圆心O到一条直线的距离为2，则这条直线可能是（ ）
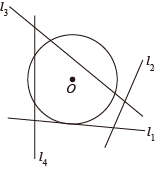A、 B、 C、 D、2. 如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2＝8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现（ ）
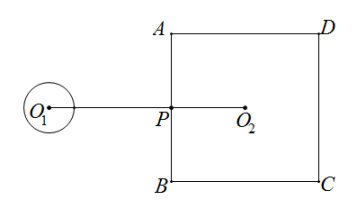A、3次 B、5次 C、6次 D、7次3. 如图，AB与⊙O相切于点B，连接OA交⊙O于点C，点D为优弧BDC上一点，连接DB，DC，若∠BDC＝30°，⊙O的半径OC＝2，则AB的长为（ ）
A、4 B、2 C、2 D、14. 若A，B为圆O上两个点，当A，B两点间优弧所对的圆周角为110°时，则圆O在A，B两点处的两条切线相交形成的锐角为（ ）A、30° B、40° C、50° D、70°5. 如图，菱形ABCD的边长为10，面积为80，∠BAD<90°，⊙O与边AB，AD都相切，菱形的顶点A到圆心O的距离为5，则⊙O的半径长等于（ ）
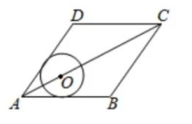A、2.5 B、 C、2 D、36. 下列命题中，假命题是（ ）A、经过半径的端点且垂直于这条半径的直线是圆的切线 B、经过直径的端点且垂直于这条直径的直线是圆的切线 C、经过圆心且垂直于切线的直线必经过切点 D、经过切点且垂直于切线的直线必经过圆心7. 如图，⊙O是△ABC的内切圆，分别切BA，BC，AC于点E，F，D，点P在弧DE上。如果∠EPF=70°，那么∠B=（ ）
A、40° B、50° C、60° D、70°8. 如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）
A、
B、π
C、2π
D、4π
9. 如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：①AD=DC；②AB=BD；③AB= BC；④BD=CD，
其中正确的个数为（ ）
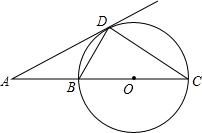A、4个 B、3个 C、2个 D、1个10. 如图，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连结AC，BC. 若∠BAC=2∠BCO，AC=3，则PA的长为（ ）
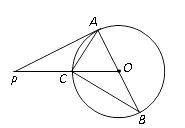A、3 B、4 C、5 D、6二、填空题
-
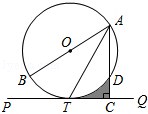
11. 如图，AB是⊙O的直径，点D、T是圆上的两点，且AT平分∠BAD，过点T作AD延长线的垂线PQ，垂足为C．若⊙O的半径为2，TC= ，则图中阴影部分的面积是 ．
12. 如图，点C在以 为直径的半圆上， ， ，点D在线段 上运动，点E与点D关于 对称， 于点D，并交 的延长线于点F.有下列结论：① ；②线段 的最小值为 ；③当 时， 与半圆相切；④若点F恰好落在弧 上，则 ；⑤当点D从点A运动到点B时，线段 扫过的面积是 ，其中正确结论的序号是.
13. 点P为⊙O外一点，直线PO与⊙O的两个公共点为A、B，过点P作⊙O的切线，点C为切点，连接AC．若∠CPO=50°，则∠CAB为 °．14. 已知⊙O的直径AB与弦AC的夹角为30°，过C点的切线PC与AB的延长线交于点P，且PC＝12，则⊙O的半径为
15. 如图，AB是⊙O的弦，AC与⊙O相切于点A，接OA，OB，若∠P＝50°，则∠BAC＝.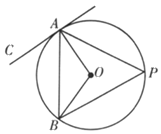
16. 在矩形ABCD中，AB＝5，BC＝12，点A在⊙B上，如果⊙D与⊙B相切，那么⊙D的半径等于 ．
三、解答题
-
17. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE＝∠C.求证：AE与⊙O相切.
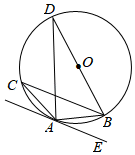18. 如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE= .求证：CB是⊙O的切线.
19. 如图，在△ABC中，AB=AC=10，BC=16，⊙A的半径为7，判断⊙A与直线BC的位置关系，并说明理由.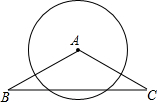
20. 如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于Q，过Q的⊙O的切线交OA的延长线于R．求证：RP=RQ．
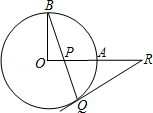21. 如图，抛物线 与 轴交于点 ， ，与 轴交于点 ，已知 .
(1)、求抛物线的函数表达式；(2)、若点 在 轴上，在该抛物线的对称轴上，是否存在唯一的点 ，满足 ？如果存在，请求出点 的坐标；如果不存在，请说明理由；(3)、若点 在 轴上，满足 的点 是否存在？如果存在，请求出点 的坐标；如果不存在，请说明理由.22. 如图， 是 的外接圆， 为直径，点 在半圆 上，且与点 在 的异侧， 交 的延长线于点 ， .
(1)、求证： ；(2)、求证： 是 的切线；(3)、若 ， ，求 .
