2022-2023学年浙教版数学九年级下册第1章解直角三角形单元检测

试卷更新日期：2022-07-25 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 计算sin 45°+cos45°的值为（）

A、1 B、2 C、 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
2. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $B C = 1$ ， $A B = 2$ ，则 $\sin A$ 的值为（）

A、 $\frac{1}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
3. 如图，滑雪场有一坡角为20°的滑道，滑雪道的长AC为100米，则BC的长为（）米．

A、 $\frac{100}{c o s 20 °}$ B、100cos20° C、 $\frac{100}{s i n 20 °}$ D、100sin20°

查看试题解析
4. 实数 $t a n 45 °$ ， $\sqrt[3]{64}$ ， $0$ ， $- π$ ， $\sqrt{9}$ ， $\frac{22}{7}$ ， $0.3131131113 \dots$ （相邻两个3之间依次多一个 1），其中无理数的个数是（）

A、4 B、2 C、1 D、3

查看试题解析
5. 如图所示，△ABC的顶点是正方形网格的格点，则sin∠A的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{10}}{10}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
6. 在下列网格中，小正方形的边长为1，点A，B，求∠A的余弦值（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{10}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图所示，正方形ABCD中， $A B = 4$ ，点E为BC中点， $B F ⊥ A E$ 于点G，交CD边于点F，连接DG，则DG长为（）

A、 $\frac{9}{5} \sqrt{5}$ B、4 C、 $\frac{16}{5}$ D、 $\frac{8}{5} \sqrt{5}$

查看试题解析
8. 如图，已知点A（ $\sqrt{3}$ ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax²+bx+1中a，b的值分别为（）

A、 $a = 2 ， b = - \frac{5}{3} \sqrt{3}$ B、 $a = \frac{1}{2} ， b = - \frac{\sqrt{3}}{6}$ C、 $a = 3 ， b = - \frac{8}{3} \sqrt{3}$ D、 $a = - \frac{1}{3} ， b = \frac{2}{3} \sqrt{3}$

查看试题解析
9. 如图，在⊙O中，弦AB的长是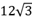 cm，弦AB的弦心距为6cm，E是⊙O优弧AEB上一点.则∠AEB的度数为（）

A、60° B、45° C、30° D、80°

查看试题解析
10. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $t a n A = \frac{4}{3}$ ，则 $s i n B$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析

二、填空题（每题4分，共24分）

11. 在Rt△ABC中，∠C＝90°，若AB＝4，sinA＝，则斜边上的高等于．

查看试题解析
12. 如图，河坝的横断面迎水坡AB的坡比是1： $\sqrt{3}$ （坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=6m，则坡面AB的长度是m.

查看试题解析
13. 已知 $∠ A$ 是锐角 $t a n A = \frac{\sqrt{3}}{2}$ ，则 $s i n A =$ .

查看试题解析
14. 如图，在4×4的正方形网格中，△ABC的顶点都在边长为1的小正方形的顶点上，则tan∠ACB的值为 .

查看试题解析
15. 如图．点E在正方形ABCD的边BC上，2BE=3CE，过点D作AE的垂线交AB于F，点G为垂足，若FG=3，则EG的长为．

查看试题解析
16. 将一架长为3米的梯子斜靠在竖直的墙AB上，梯子与地面的夹角 $∠ B C A = 65 °$ ，则梯子底端C与墙根A点的距离为米．（结果精确到 $0.1$ 米）[参考数据： $s i n 65 ° \approx 0.91$ ， $c o s 65 ° \approx 0.42$ ， $t a n 65 ° \approx 2.14$ ]

查看试题解析

三、解答题（共8题，共66分）

17. 如图，升国旗时，某同学站在离国旗20m的E处行注目礼（即BE=20m），当国旗升至旗杆顶端A时，该同学视线的仰角∠ADC=42°，已知他的双眼离地面的高度DE=1.60m．求旗杆AB的高度（结果精确到0.01m）．
参考数据：sin42°≈0.6691，cos42°≈0.7431，tan42°≈0.9004．

查看试题解析
18. 先化简，再求代数式 $\frac{x + 1}{x} \div (x - \frac{x^{2} + 1}{2 x})$ 的值，其中 $x = 2 s i n 30 ° + t a n 60 °$ ．

查看试题解析
19. 先化简，再求代数式 $\frac{m^{2} - 2 m + 1}{m^{3} - m} \div \frac{m - 1}{m}$ 的值，其中 $m = t a n 60 ° - 2 s i n 30 °$

查看试题解析
20. 先化简，再求代数式 $\frac{x - 3}{2 x + 4} \div (x - 2 - \frac{5}{x + 2})$ 的值，其中 $x = c o s 30 ° - 3 t a n 45 °$ ．

查看试题解析
21. 如图大金鹰雕塑用线段MN表示，雄居在重庆南山鹞鹰岩上且垂直于地面，水泥浇铸，重千吨，外敷金箔，内设通道，游客可直登鹰的头部，上设有观景台，凭栏远眺，重庆数十里景物尽收眼底.如图，小明沿坡度 $i = 1 ： 2.4$ 的斜坡AN登山浏览大金鹰，小明在坡脚A测得大金鹰顶部M的仰角为45°，然后沿坡面AN行走52米到达B处，在B处测得大金鹰顶部M的仰角为60°（点A、B、M、N均在同一平面内）.（结果精确到1米，参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ）

(1)、求B处的竖直高度；

(2)、求大金鹰MN的高.

查看试题解析
22. 如图，建筑物 $A B$ 后有一座小山， $∠ D C F = 30 °$ ，测得小山坡脚C点与建筑物水平距离 $B C = 25$ 米，若山坡上E点处有一凉亭，且凉亭与坡脚距离 $C E = 20$ 米，某人从建筑物顶端A点测得E点处的俯角为 $48 °$ .

(1)、求凉亭到地面的距离；

(2)、求建筑物 $A B$ 的高.（精确到 $0.1 m$ ）
（参考数据： $\sqrt{3} \approx 1.73$ ， $s i n 48 ° \approx 0.74$ ， $c o s 48 ° \approx 0.67$ ， $t a n 48 ° \approx 1.11$ ， $s i n 42 ° \approx 0.67$ ， $c o s 42 ° \approx 0.74$ ， $t a n 42 ° \approx 0.90$ ）

查看试题解析
23. 图1，图2分别是某型号拉杆箱的实物图与平面示意图，具体信息如下：水平滑杆 $DE$ 、箱长 $BC$ 、拉杆 $AB$ 的长度都相等，即 $DE = BC = AB$ ，点 $B$ ， $F$ 在线段 $AC$ 上，点 $C$ 在 $DE$ 上，支撑点 $F$ 到箱底 $C$ 的距离 $FC = 32 cm$ ， $CE$ ： $CD = 1$ ： $5$ ， $DF ⊥ AC$ 于点 $F$ ， $∠ DCF = 50 °$ ，请根据以上信息，解决下列问题：

(1)、求水平滑杆 $DE$ 的长度；

(2)、求拉杆端点 $A$ 到水平滑杆 $DE$ 的距离 $h$ 的值 $($ 结果保留到 $1 cm) . ($ 参考数据： $sin 50 ° \approx 0.77$ ， $cos 50 ° \approx 0.64$ ， $tan 50 ° \approx 1.19)$ .

查看试题解析
24. 如图，在菱形ABCD中，AB=3，∠B=60°，AC为对角线，点E、F分别在边AB、BC上（不与端点重合），且AE=BF，连接CE、AF交于点G.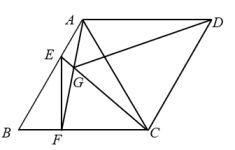

(1)、求证：△ABF≌△CAE；

(2)、求∠FGC的度数；

(3)、连接EF，DG，若EF⊥BC，求线段DG的长.

查看试题解析

2022-2023学年浙教版数学九年级下册第1章 解直角三角形 单元检测

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022-2023学年浙教版数学九年级下册第1章解直角三角形单元检测