2022-2023学年浙教版数学九年级下册1.3 解直角三角形 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 如图是大坝的横断面,斜坡AB的坡度 i1 =1:2,背水坡CD的坡度i2=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )
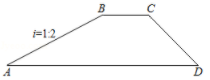 A、 B、 C、 D、242. 如图,冬奥会滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则BC的长为( )米.
A、 B、 C、 D、242. 如图,冬奥会滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则BC的长为( )米. A、 B、 C、 D、3. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )
A、 B、 C、 D、3. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )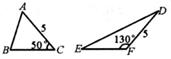 A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能4. 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能4. 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )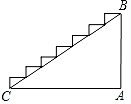 A、3.5sin29° B、3.5cos29° C、3.5tan29° D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )
A、3.5sin29° B、3.5cos29° C、3.5tan29° D、5. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )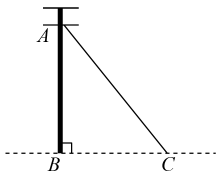 A、米 B、米 C、米 D、米6. 已知一道斜坡的坡比为1: ,坡长为24米,那么坡高为( )米.A、 B、12 C、 D、67. 如图所示,河堤横断面迎水坡AB的坡比是 ,堤高 ,则坡面AB的长度是( )m
A、米 B、米 C、米 D、米6. 已知一道斜坡的坡比为1: ,坡长为24米,那么坡高为( )米.A、 B、12 C、 D、67. 如图所示,河堤横断面迎水坡AB的坡比是 ,堤高 ,则坡面AB的长度是( )m A、8 B、16 C、 D、8. 如图,点A到点C的距离为100米,要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( )
A、8 B、16 C、 D、8. 如图,点A到点C的距离为100米,要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( ) A、100米 B、50米 C、米 D、50米9. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A、100米 B、50米 C、米 D、50米9. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )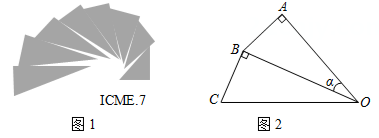 A、 B、 C、 D、10. 在 中,∠C= ,AB=4, ,则 的长为( )A、3 B、2 C、 D、
A、 B、 C、 D、10. 在 中,∠C= ,AB=4, ,则 的长为( )A、3 B、2 C、 D、二、填空题
-
11. 平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A为 , ∠B为 , 边AB的长为2m,BC边上露出部分BD的长为0.9m,则铁板BC边被掩埋部分CD的长是m.(参考数据: , , ).
 12. 如图,在中,弦的长为 , 圆心到弦的距离为6,则的度数为.
12. 如图,在中,弦的长为 , 圆心到弦的距离为6,则的度数为.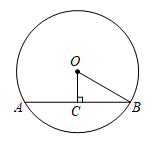 13. 如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米.
13. 如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米. 14. 如图,已知斜坡AC的坡度i=1:2,小明沿斜坡AC从点A行进10m至点B,在这个过程中小明升高 m.
14. 如图,已知斜坡AC的坡度i=1:2,小明沿斜坡AC从点A行进10m至点B,在这个过程中小明升高 m. 15. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.则大楼AB的高度 .(结果保留根号)
15. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.则大楼AB的高度 .(结果保留根号)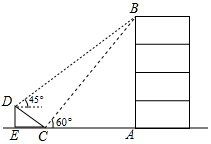 16. 某通信公司准备逐步在山上建设5G基站.如图,某处斜坡的坡角的正切值为 , 通讯塔垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段长26米则通讯塔的高度约为米.(参考数据: , , )
16. 某通信公司准备逐步在山上建设5G基站.如图,某处斜坡的坡角的正切值为 , 通讯塔垂直于水平地面,在C处测得塔顶A的仰角为45°,在D处测得塔顶A的仰角为53°,斜坡路段长26米则通讯塔的高度约为米.(参考数据: , , )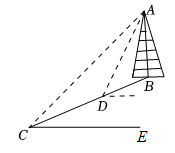
三、解答题
-
17. 某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
课题
测量嵩岳寺塔的高度
测量工具
测量角度的仪器,皮尺等
测量方案
在点 处放置高为 米的测角仪 ,此时测得塔顶端 的仰角为 ,再沿 方向走 米到达点 处,此时测得塔顶端 的仰角为 .
说明: 、 、 三点在同一水平线上
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔 的高度.
精确到0.1米,参考数据: , ,
 18. 如图,小丽家住在巴河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC. 为了测量大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为45°,爬上楼顶D处得大厦顶部B的仰角为30°. 已知小丽家所住的电梯公寓高36米,请你帮助小丽计算出大厦高度BC,结果保留整数.(参考数据: , )
18. 如图,小丽家住在巴河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC. 为了测量大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为45°,爬上楼顶D处得大厦顶部B的仰角为30°. 已知小丽家所住的电梯公寓高36米,请你帮助小丽计算出大厦高度BC,结果保留整数.(参考数据: , ) 19. 扬州中国大运河博物馆坐落于扬州三湾古运河畔,大运河博物馆整体由大运塔和博物馆主体两部分组成.周末汐汐和父母去大运河博物馆游玩,看到大运塔时觉得非常宏伟,想知道它的高度.于是汐汐走到点C处,测得此时塔尖A的仰角是37°,向前走了40米至点E处,测得此时塔尖A的仰角是45°,已知汐汐的眼睛离地面高度是1.2米,请聪明的你帮她求出塔AB的高度.(参考数据:sin37°≈ , cos37°≈ , tan37°≈)
19. 扬州中国大运河博物馆坐落于扬州三湾古运河畔,大运河博物馆整体由大运塔和博物馆主体两部分组成.周末汐汐和父母去大运河博物馆游玩,看到大运塔时觉得非常宏伟,想知道它的高度.于是汐汐走到点C处,测得此时塔尖A的仰角是37°,向前走了40米至点E处,测得此时塔尖A的仰角是45°,已知汐汐的眼睛离地面高度是1.2米,请聪明的你帮她求出塔AB的高度.(参考数据:sin37°≈ , cos37°≈ , tan37°≈) 20. 在一次户外综合实践活动中,九年级数学兴趣小组用无人机航拍测量公园内一条笔直的骑行步道AB的长度.由于无人机控制距离有限,为了安全,不能直接测量,他们采用如下方法:如图,在起点A的正上方点C处测得终点B的俯角α=17.1°;接着无人机往终点B方向水平飞行0.9km到达点D处, 此时测得终点B的俯角β=45°.求骑行步道AB的长度.(结果精确到0.1km,参考数据:sin17.1°≈0.29,cos17.1°≈0.96,tan17.1°≈0.31,)
20. 在一次户外综合实践活动中,九年级数学兴趣小组用无人机航拍测量公园内一条笔直的骑行步道AB的长度.由于无人机控制距离有限,为了安全,不能直接测量,他们采用如下方法:如图,在起点A的正上方点C处测得终点B的俯角α=17.1°;接着无人机往终点B方向水平飞行0.9km到达点D处, 此时测得终点B的俯角β=45°.求骑行步道AB的长度.(结果精确到0.1km,参考数据:sin17.1°≈0.29,cos17.1°≈0.96,tan17.1°≈0.31,)
四、综合题
-
21. 如图,在矩形中,点E为边上的一动点(点E不与点A,B重合),连接 , 过点C作 , 垂足为F.
 (1)、求证:∽;(2)、若 , , 求的长.22. 在一次课外活动中,某数学兴趣小组测量一棵树CD的高度.如图所示,测得斜坡BE的坡度i=1:4(即AB:AE=1:4),坡底AE的长为8米,在B处测得树CD顶部D的仰角为30°,在E处测得树CD顶部D的仰角为60°.
(1)、求证:∽;(2)、若 , , 求的长.22. 在一次课外活动中,某数学兴趣小组测量一棵树CD的高度.如图所示,测得斜坡BE的坡度i=1:4(即AB:AE=1:4),坡底AE的长为8米,在B处测得树CD顶部D的仰角为30°,在E处测得树CD顶部D的仰角为60°.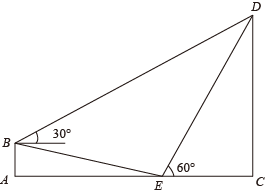 (1)、求AB的高;(2)、求树高CD.(结果保留根号)23. 图(1)为某大型商场的自动扶梯.图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL( )向正前方走了2m,发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m,(参考数据:sin37°≈0.6,cos37°=0.8,tan37°≈0.75).
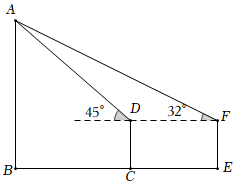
(1)、求AB的高;(2)、求树高CD.(结果保留根号)23. 图(1)为某大型商场的自动扶梯.图(2)中的AB为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点A处时,测得天花板上日光灯C的仰角为37°,此时他的眼睛D与地面的距离AD=1.8m,之后他沿一楼扶梯到达顶端B后又沿BL( )向正前方走了2m,发现日光灯C刚好在他的正上方.已知自动扶梯AB的坡度为1:2.4,AB的长度是13m,(参考数据:sin37°≈0.6,cos37°=0.8,tan37°≈0.75). (1)、求图中B到一楼地面的高度.(2)、求日光灯C到一楼地面的高度.(结果精确到十分位).24. 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,
(1)、求图中B到一楼地面的高度.(2)、求日光灯C到一楼地面的高度.(结果精确到十分位).24. 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m, (1)、若F与BC相距12m,求建筑物BC的高度;(2)、若旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(参考数据: ≈1.414,sin52°≈0.788,tan52°≈1.280).
(1)、若F与BC相距12m,求建筑物BC的高度;(2)、若旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(参考数据: ≈1.414,sin52°≈0.788,tan52°≈1.280).