2022-2023学年浙教版数学九年级下册1.2 锐角三角函数的计算 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 如图,已知:45°<∠A<90°,则下列各式成立的是( )
 A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA2. 已知β为锐角,cos β≤ ,则β的取值范围为( )
A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA2. 已知β为锐角,cos β≤ ,则β的取值范围为( )
A、30°≤β<90° B、0°<β≤60° C、60°≤β<90° D、30°≤β<60°3. 四位学生用计算器求cos 27°40'的近似值的结果如下,正确的是( )
A、0.885 7 B、0.885 6 C、0.885 2 D、0.885 14. 已知β为锐角,且tan β=3.387,则β约等于( )
A、73°33' B、73°27' C、16°27' D、16°21'5. 用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )A、tan 25°<cos 26°<sin 27° B、tan 25°<sin 27°<cos 26° C、sin 27°<tan 25°<cos 26° D、cos 26°<tan 25°<sin 27°6. 用科学计算器求sin 9°的值,以下按键顺序正确的是( )A、sin9= B、9sin= C、sin9 D、9sin7. 在△ABC中,∠C=90°,BC=5,AB=13,用科学计算器求∠A约等于( )
A、24°38' B、65°22' C、67°23' D、22°37'8. 如果∠A为锐角,cos A= ,那么( )A、0°<∠A<30° B、30°<∠A<45° C、45°<∠A<60° D、60°<∠A<90°9. 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )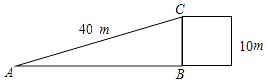 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
10. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )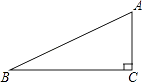 A、
A、 B、
B、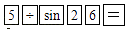 C、
C、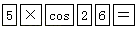 D、
D、
二、填空题
-
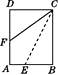
11. 比较大小:sin35°cos45°.12. 已知 ,且 为锐角,则m的取值范围是 .13. 如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,展开后,若AB∶BC=4∶5,则∠CFD≈.(精确到0.01°)
 14. 比较下列各对数的大小,并提出你的猜想:
14. 比较下列各对数的大小,并提出你的猜想:①sin30° 2sin15°cos15°;
②sin36° 2sin18°cos18°;
③sin45° 2sin22.5°cos22.5°;
④sin60° 2sin30°cos30°;
⑤sin80° 2sin40°cos40°.
猜想:已知0°<α<45°,则sin2α 2sinαcosα.
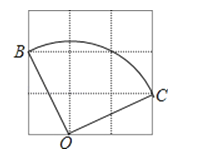
15. 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.A、如图,在3×3的方格中(共有9个小格),每个小方格都是边长为1的正方形,O、B、C是格点,则扇形OBC的面积等于
B、用科学计算器计算:133sin18°= (结果精确到0.1)
 16. 请从以下两个小题中任选一题作答,若多选,则按第一题计分.
16. 请从以下两个小题中任选一题作答,若多选,则按第一题计分.儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,能比标价省13.2元,已知书包标价比文具盒标价的3倍少6元.那么设一个文具盒标价为x元,依据题意列方程得
三、解答题
-
17. 设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论.18. 已知sin A=0.328 6,tan B=10.08,利用计算器求锐角A,B.(结果精确到0.01°)19. 已知,凸4n+2边形A1A2…A4n+2(n是非零自然数)各内角都是30°的整数倍,又关于x的方程:
均有实根,求这凸4n+2边形各内角的度数.
20. 已知:如图,在△ABC中,AB=8,AC=9,∠A=48°.求:AB边上的高(精确到0.01);
 21.(1)、完成下列表格,并回答下列问题,
21.(1)、完成下列表格,并回答下列问题,锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .22. 如图①②,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律. (1)、根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.(2)、比较大小(在横线上填写“<”“>”或“=”):
(1)、根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.(2)、比较大小(在横线上填写“<”“>”或“=”):若α=45°,则sin α cos α;
若α<45°,则sin α cos α;
若α>45°,则sin α cos α.
(3)、利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.
23. 如图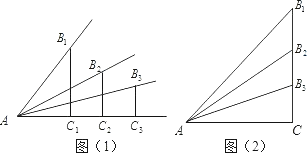 (1)、如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;(2)、根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;(3)、比较大小:(在空格处填写“<”或“>”或“=”)
(1)、如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;(2)、根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;(3)、比较大小:(在空格处填写“<”或“>”或“=”)若∠α=45°,则sinαcosα;若∠α<45°,则sinαcosα;若∠α>45°,则sinαcosα;
(4)、利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:sin10°,cos30°,sin50°,cos70°.
24. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF. (1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.
(1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.