2022年浙教版数学八年级上学期第5章一次函数单元检测

试卷更新日期：2022-07-25 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 一次函数 $y = k x + k$ ，当系数 $k < 0$ 时，其图象大致是（）

A、 B、 C、 D、

查看试题解析
2. 在一次函数y=2x-1图象上的点是（）

A、(2，3) B、(0，1) C、(1，0) D、(-1，1)

查看试题解析
3. 已知点 $A (- 2 ， y_{1})$ ， $B (3 ， y_{2})$ 在一次函数 $y = - 2 x + b$ 的图象上，则 $y_{1}$ ， $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、以上都不对

查看试题解析
4. 已知一次函数 $y = k x + 1$ 的图象经过点A，且y随x的增大而减小，则点A的坐标可能为（）

A、 $(- 2 ， 0)$ B、 $(2 ， 0)$ C、 $(- 1 ， 0)$ D、 $(1 ， 2)$

查看试题解析
5. EF是BC的垂直平分线，交BC于点D，点A是直线EF上一动点，它从点D出发沿射线DE方向运动，当 $∠ B A C$ 减少 $x °$ 时， $∠ A B C$ 增加 $y °$ ，则y与x的函数表达式是（）

A、 $y = x$ B、 $y = \frac{1}{2} x$ C、 $y = 90 - x$ D、 $y = 90 - \frac{1}{2} x$

查看试题解析
6. 已知点 $(x_{1} ， - 3)$ ， $(x_{2} ， 4)$ 都在直线 $y = - 2 x + 1$ 上，则 $x_{1}$ 与 $x_{2}$ 的大小关系为（）

A、 $x_{1} > x_{2}$ B、 $x_{1} = x_{2}$ C、 $x_{1} < x_{2}$ D、无法比较

查看试题解析
7. 如图，已知直线 $y = \frac{1}{2} x - 1$ 与x轴交于点A，与y轴交于点B，以点B为圆心、 $A B$ 长为半径画弧，与y轴正半轴交于点C，则点C的坐标为（）

A、 $(0 ， \sqrt{5})$ B、 $(0 ， \sqrt{5} + 1)$ C、 $(0 ， \sqrt{5} - 1)$ D、 $(0 ， 1 - \sqrt{5})$

查看试题解析
8. 如图，已知点K为直线I：y=2x+4上一点，先将点K向下平移2个单位，再向左平移a个单位至点K₁ ，然后再将点K₁向上平移b个单位，向右平1个单位至点K₂ ，若点K₂也恰好落在直线l上，则a，b应满足的关系是（ )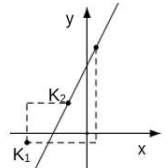

A、a+2b=4 B、2a-b=4 C、2a+b=4 D、a+b=4

查看试题解析
9. 已知点 $A (m - 1 ， y_{1})$ 和点 $B (m + 1 ， y_{2})$ 在一次函数 $y = (k + 2) x + 1$ 的图象上，且y₁>y₂ ，下列四个选项中k的值可能是（ )

A、-3 B、-1 C、1 D、3

查看试题解析
10. 在同一直角坐标系中，一次函数y＝kx＋k与正比例函数y＝kx的图像可能是（）

A、 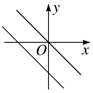B、 C、 D、

查看试题解析

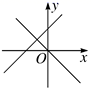
二、填空题（每题4分，共24分）

11. 指出下列事件过程中的常量与变量.

(1)、某水果店橘子的单价为5元／千克，买a千克橘子的总价为m元，其中常量是，变量是；

(2)、周长C与圆的半径r之间的关系式是C＝2πr，其中常量是，变量是；
注意：π是一个确定的数，是常量

查看试题解析
12. 圆的半径为 $r$ ，圆的面积 $S$ 与半径 $r$ 之间有如下关系： $S = π r^{2}$ .在这关系中，常量是.

查看试题解析
13. 将函数y＝3x－4 的图象向上平移5个单位长度，所得图象对应的函数表达式为.

查看试题解析
14. 一次函数y＝（k+5）x﹣2中y随x的增大而减小，则k的取值范围是.

查看试题解析
15. 在平面直角坐标系xOy中，一次函数y＝kx+b（k≠0，k，b均为常数）与正比例函数y＝﹣ $\frac{1}{3}$ x的图象如图所示，则关于x的不等式kx+b＞﹣ $\frac{1}{3}$ x的解集为.

查看试题解析
16. 如图，一次函数y＝kx+b的图象与x轴交于点A（3，0），与y轴交于点B（0，4），与正比例函数y＝ax的图象交于点C，且点C的横坐标为2，则不等式ax＜kx+b的解集为．

查看试题解析

三、解答题（共8题，共66分）

17. 已知函数 $y = (2 m + 1) x + m - 3$

(1)、若函数图象经过原点，求 $m$ 的值；

(2)、若函数的图象平行于直线 $y = 3 x - 3$ ，求 $m$ 的值

(3)、若这个函数是一次函数，且 $y$ 随着 $x$ 的增大而增大，且不经过第二象限，求 $m$ 的取值范围．

查看试题解析
18. 已知：如图，正比例函数 $y = 2 x$ 和一次函数 $y = - \frac{2}{3} x + 4$ 的图象相交于点 $A (\frac{3}{2} ， 3)$ ，且一次函数 $y = - \frac{2}{3} x + 4$ 的图象与 $x$ 轴交于点 $B$ .

(1)、求点 $B$ 的坐标；

(2)、求 $△ A O B$ 的面积.

查看试题解析
19. 某地出租车计费方法如图所示， $x (km)$ 表示行驶里程，y（元）表示车费，请根据图象回答下面的问题：

(1)、该地出租车的起步价是元；

(2)、当 $x > 3$ 时，求y关于x的函数关系式；

(3)、若某乘客一次乘出租车的车费为40元，求这位乘客乘车的里程.

查看试题解析
20. 我国是一个严重缺水的国家，大家应该倍加珍惜水资源，节约用水.据测试，拧不紧的水龙头每秒会滴下2滴水，每滴水约0.05 mL.小明同学在洗手时，没有把水龙头拧紧，当小明离开x h后，水龙头滴了y mL水.

(1)、试写出y与x之间的函数解析式；

(2)、当滴了1620 mL水时，小明离开水龙头多长时间？

查看试题解析
21. A、B两地相距60km.甲、乙两车从A地出发去B地，乙车的速度是甲车速度的4倍，甲车比乙车早1h出发.甲、乙两车距离A地的路程y（km）与乙车出发的时间x（h）之间的函数关系如图①所示.

(1)、甲车的速度是km/h；

(2)、乙车出发几小时后追上甲车？

(3)、设两车之间的距离为s km，甲车行驶的时间为t h，在图②的平面直角坐标系中画出s与t的函数图象（请标出必要的数据）.

查看试题解析
22. 如图，公路上有A、B、C三个汽车站，一辆汽车8：00从离C站340km的A站出发，向C站匀速行驶，15min后离C站320km.

(1)、设出发xh后，汽车离C站ykm，则y与x之间的函数表达式为；

(2)、当汽车行驶到离C站还有100km的B站时，司机接到通知要在12：00前赶到离C站190km的服务区P（在A、B之间）.汽车按原速行驶，能否准时到达？说明理由.

查看试题解析
23. 如图，已知 $A (8 ， m)$ 为正比例函数 $y = \frac{3}{4} x$ 的图象上一点， $A B ⊥ x$ 轴，垂足为点B.

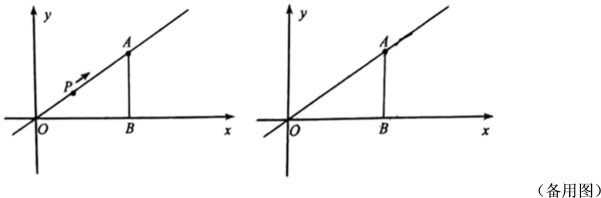(1)、求m的值；

(2)、点P从O出发，以每秒 $2$ 个单位的速度，沿射线 $O A$ 方向运动.设运动时间为 $t$ $(s)$ .
①过点P作 $P Q ⊥ O A$ 交直线 $A B$ 于点Q，若 $Δ A P Q ≅ Δ A B O$ ，求t的值；
②在点P的运动过程中，是否存在这样的t，使得 $Δ P O B$ 为等腰三角形？若存在，请求出所有符合题意的t的值；若不存在，请说明理由.

查看试题解析

2022年浙教版数学八年级上学期第5章 一次函数 单元检测

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022年浙教版数学八年级上学期第5章一次函数单元检测