2022-2023学年浙教版数学八年级上册5.5 一次函数的简单应用 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
 A、1 B、2 C、3 D、42. 已知一次函数y1=kx+1和y2=x﹣2.当x<1时,y1>y2 , 则k的值可以是( )A、-3 B、-1 C、2 D、43. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.
A、1 B、2 C、3 D、42. 已知一次函数y1=kx+1和y2=x﹣2.当x<1时,y1>y2 , 则k的值可以是( )A、-3 B、-1 C、2 D、43. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则18分钟时的温度是( )
A、62℃ B、64℃ C、66℃ D、68℃4. 如图,一次函数y=ax+b的图象与y=cx+d的图象如图所示且交点的横坐标为4,则下列说法正确的个数是( )
①对于函数y=ax+b来说,y随x的增大而减小;②函数y=ax+d不经过第一象限;③方程ax+b=cx+d的解是x=4;④ d-b=4(a-c).
A、1 B、2 C、3 D、45. 巴中某快递公司每天上午7:00﹣8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为( )①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为8件;
③8:00时,甲仓库内快件数为400件;
④7:20时,两仓库快递件数相同.
 A、1个 B、2个 C、3个 D、4个6. 如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( )
A、1个 B、2个 C、3个 D、4个6. 如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( ) A、15元 B、20元 C、25元 D、30元7. 一个装有进水管和出水管的容器,开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图,则8分钟时容器内的水量(单位:升)为( )
A、15元 B、20元 C、25元 D、30元7. 一个装有进水管和出水管的容器,开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图,则8分钟时容器内的水量(单位:升)为( )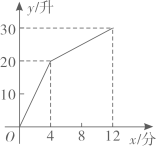 A、24 B、25 C、26 D、278. 已知一次函数与一次函数中,函数、与自变量x的部分对应值分别如表1、表2所示:
A、24 B、25 C、26 D、278. 已知一次函数与一次函数中,函数、与自变量x的部分对应值分别如表1、表2所示:表1:
x
…
0
1
…
…
3
4
…
表2:
x
…
0
1
…
…
5
4
3
…
则关于x的不等式的解集是( )
A、 B、 C、 D、9. 甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min 再以原速返回A地,当两人到达A地后停止骑行.设甲出发x min后距离A地的路程为y km.图中的折线表示甲在整个骑行过程中y与x的函数关系.在整个骑行过程中,两人只相遇了1次,乙的骑行速度(单位:km/min)可能是( ) A、0.1 B、0.15 C、0.2 D、0.2510. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( )
A、0.1 B、0.15 C、0.2 D、0.2510. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息、已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相聚180米有2个时刻,分别是t=18和t=24.其中正确的结论有( ) A、①② B、①③ C、②④ D、①②④
A、①② B、①③ C、②④ D、①②④二、填空题
-
11. 在平面直角坐标系中,一次函数 ( 是常数, )与 (m、n是常数, )的图象如图所示,则关于x的不等式 的解集为.
 12. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费y(元)与行李质量 之间满足一次函数关系,部分对应值如下表:
12. 某长途汽车客运公司规定旅客可免费携带一定质量的行李.当行李的质量超过规定时,需付的行李费y(元)与行李质量 之间满足一次函数关系,部分对应值如下表:…
30
40
50
…
y(元)
…
4
6
8
…
则旅客最多可免费携带行李的质量是kg.
13. 已知一次函数y=ax+b和y=kx的图象交于点P(﹣4,2),则关于x、y的二元一次方程组 的解是.14. 如图,一次函数 与 的图象相交于点 ,则关于x的不等式 的解集为. 15. 如图,已知直线l1:y=3x+1和直线l1:y=mx+n交于点P(1,b),则关于x,y的二元一次方程组 的解是 .
15. 如图,已知直线l1:y=3x+1和直线l1:y=mx+n交于点P(1,b),则关于x,y的二元一次方程组 的解是 .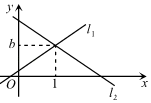 16. 若函数 的图象经过点 ,其图象如图所示,则关于x的不等式 的解集为.
16. 若函数 的图象经过点 ,其图象如图所示,则关于x的不等式 的解集为.
三、解答题
-
17. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.
 (1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围.
(1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围. 19. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.20. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?
19. 已知: , 与 成正比例, 与x成反比例.当 时, ;当 时, .求y与x的函数解析式.20. 甲,乙两地相距300千米.一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,线段CD对应的函数解析式是y=110x﹣195(2.5≤x≤4.5),在轿车行进过程中,轿车行驶多少时间,两车相距15千米?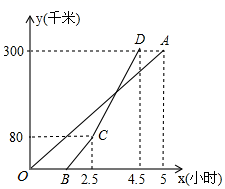 21. 我省要按照城市功能特点,城区消费到2022年,建设20个省内特色消费中心,着力发展“夜经济”,打造郑州“夜商都”等地方夜消费品牌升级版.允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两款特价商品,两款商品的进价与售价如表所示:
21. 我省要按照城市功能特点,城区消费到2022年,建设20个省内特色消费中心,着力发展“夜经济”,打造郑州“夜商都”等地方夜消费品牌升级版.允许市场经营主体在规范有序的条件下,采取“店铺外摆”“露天市场”方式进行销售.个体业主小王响应号召,采取“店铺外摆”方式销售甲、乙两款特价商品,两款商品的进价与售价如表所示:甲商品
乙商品
进价(元/件)
35
5
售价(元/件)
45
8
小王计划购进甲、乙两种商品共100件进行销售.设小王购进甲商品 件,甲、乙商品全部销售完后获得的利润为 元.
(1)、求出 与 之间的函数关系式;(2)、若购进乙商品的件数不少于甲商品件数的3倍,当购进甲,乙两种商品各多少件时,可使得甲、乙商品全部销售完后获得的利润最大?22. 已知y是x的一次函数,且当 时, ;当 时, .(1)、求这个一次函数的解析式;(2)、当 时,求函数y的值;(3)、当 时,求自变量x的取值范围.23. 在平面直角坐标系中,对于 、 两点,用以下方式定义两点间的“极大距离” ;若 ,则 ;若 ,则 .例如:如图,点 ,则 . (1)、(理解定义)
(1)、(理解定义)
若点 、 ,则 .(2)、在点 、 、 、 中,到坐标原点O的“极大距离”是2的点是.(填写所有正确的字母代号)(3)、(深入探索)
已知点 , ,O为坐标原点,求a的值.(4)、(拓展延伸)
经过点 的一次函数 (k、b是常数, )的图象上是否存在点P,使 ,O为坐标原点,直接写出点P的个数及对应的k的取值范围.24. A、B两地相距60km.甲、乙两车从A地出发去B地,乙车的速度是甲车速度的4倍,甲车比乙车早1h出发.甲、乙两车距离A地的路程y(km)与乙车出发的时间x(h)之间的函数关系如图①所示. (1)、甲车的速度是km/h;(2)、乙车出发几小时后追上甲车?(3)、设两车之间的距离为s km,甲车行驶的时间为t h,在图②的平面直角坐标系中画出s与t的函数图象(请标出必要的数据).
(1)、甲车的速度是km/h;(2)、乙车出发几小时后追上甲车?(3)、设两车之间的距离为s km,甲车行驶的时间为t h,在图②的平面直角坐标系中画出s与t的函数图象(请标出必要的数据).