2022-2023学年浙教版数学八年级上册5.2 函数 同步练习
试卷更新日期:2022-07-25 类型:同步测试
一、单选题
-
1. 函数y= 中,自变量x的取值范围是( )A、x≤5 B、x<5 C、x≥5 D、x>52. 当时,函数的值等于( )A、 B、 C、 D、3. 当时,函数的值是( )A、2 B、 C、 D、4. 下列关于变量x,y的关系,其中y不是x的函数的是( )A、
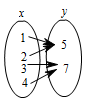 B、
B、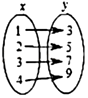 C、
C、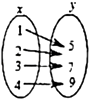 D、
D、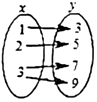 5. 下列图象表示的两个变量间的关系中,y不是x的函数的是( )A、
5. 下列图象表示的两个变量间的关系中,y不是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列函数中,自变量的取值范围选取错误的是( )A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数 C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数7. 一次函数 的自变量的取值增加2,函数值就相应减少4,则k的值为( )A、2 B、-1 C、-2 D、48. 当时,函数的值是( )A、 B、 C、2 D、19. 在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )A、
6. 下列函数中,自变量的取值范围选取错误的是( )A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数 C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数7. 一次函数 的自变量的取值增加2,函数值就相应减少4,则k的值为( )A、2 B、-1 C、-2 D、48. 当时,函数的值是( )A、 B、 C、2 D、19. 在某火车站托运物品时,不超过3kg的物品需付1.5元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是( )A、 B、
B、 C、
C、 D、
D、 10. 已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )A、y=10﹣2x(5<x<10) B、y=10﹣2x(2.5<x<5) C、y=10﹣2x(0<x<5) D、y=10﹣2x(0<x<10)
10. 已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )A、y=10﹣2x(5<x<10) B、y=10﹣2x(2.5<x<5) C、y=10﹣2x(0<x<5) D、y=10﹣2x(0<x<10)二、填空题
-
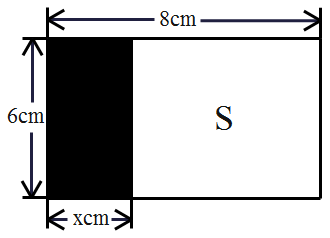
11. 函数y=-2x+6,当函数值y=4时,自变量x的值是12. 函数y= 中自变量x的取值范围是 .13. 函数 的自变量x取值范围是 .14. 已知函数y= , 当x=时,y= .15. 如果 , y=2,那么x =16. 如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为.
三、解答题
-
17. 已知函数y= 中,当x=a时的函数值为1,试求a的值.18. 在国内投寄平信应付邮资如表:
信件质量x(克)
0<x≤20
20<x≤40
40<x≤60
邮资y(元/封)
1.20
2.40
3.60
(1)、根据函数的定义,y是关于x的函数吗?(2)、结合表格解答:①求出当x=48时的函数值,并说明实际意义.
②当寄一封信件的邮资是2.40元时,信件的质量大约是多少克?
19.如图,正方形ABCD的边长为4,P为CD边上一点(与点D不重合).设DP=x,△APD的面积y关于x的函数关系式.
 20. 在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
20. 在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
21. 当x=2及x=﹣3时,分别求出下列函数的函数值:(1)y=(x+1)(x﹣2);
(2)y= .
22. 地壳的厚度约为8到40km,在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.
(1)、在这个变化过程中,自变量和因变量分别是什么?(2)、如果地表温度为2℃,计算当x为5km时地壳的温度.